题目内容
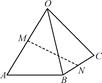
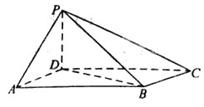
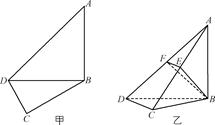
已知四棱锥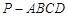 的底面为直角梯形,
的底面为直角梯形,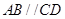 ,
,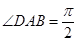 ,
, 底面
底面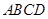 ,且
,且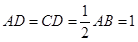 ,
,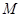 是
是 的中点.
的中点.
⑴求证:直线 平面
平面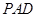 ;
;
⑵⑵若直线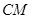 与平面
与平面 所成的角为
所成的角为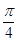 ,求二面角
,求二面角 的余弦值.
的余弦值.
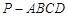 的底面为直角梯形,
的底面为直角梯形,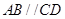 ,
,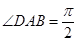 ,
, 底面
底面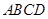 ,且
,且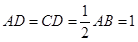 ,
,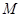 是
是 的中点.
的中点.⑴求证:直线
 平面
平面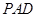 ;
;⑵⑵若直线
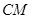 与平面
与平面 所成的角为
所成的角为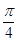 ,求二面角
,求二面角 的余弦值.
的余弦值.⑴见解析;⑵1
试题分析:方法一:几何法证明求角.
⑴要证直线
 平面
平面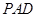 ,需要在平面
,需要在平面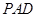 内找到一条与
内找到一条与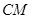 平行的直线.显然不容易找到;故考虑利用面面平行退出线面平行, 取
平行的直线.显然不容易找到;故考虑利用面面平行退出线面平行, 取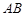 的中点
的中点 ,构造平面
,构造平面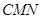 ,根据
,根据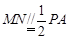 ,
,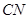 ∥
∥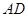 可证.
可证.⑵要求二面角,方法一:找到二面角的平面角,角的顶点在棱
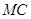 ,角的两边在两个半平面内
,角的两边在两个半平面内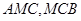 中,并且角的两边与棱垂直.取取
中,并且角的两边与棱垂直.取取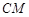 的中点
的中点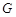 ,连接
,连接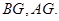
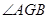 就是所求角.
就是所求角.方法二:建立空间直角坐标系,利用向量证明,求角.
试题解析:
⑴证明:取
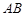 的中点
的中点 ,则
,则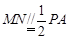 ,故
,故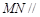 平面
平面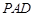 ;
;又四边形
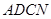 正方形,∴
正方形,∴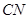 ∥
∥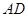 ,故
,故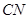 ∥平面
∥平面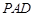 ;
;∴平面
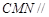 平面
平面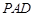 ,
,∴
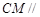 平面
平面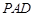 .
.⑵由
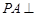 底面
底面 ,得
,得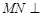 底面
底面 ;
;则
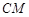 与平面
与平面 所成的角为
所成的角为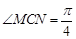 ;
;∴
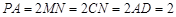 , ∴
, ∴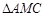 和
和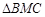 都是边长为
都是边长为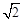 正三角形,
正三角形,取
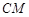 的中点
的中点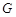 ,则
,则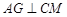 ,且
,且 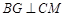 .
.
∴
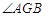 为二面角
为二面角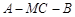 的平面角
的平面角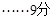 ;在
;在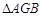 中
中 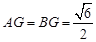 ,
,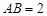 ,
,∴
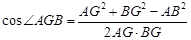
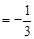
∴二面角
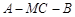 的余弦值
的余弦值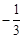
方法二:⑴设
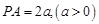 ,因为
,因为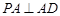 ,
, ,
,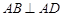 ,
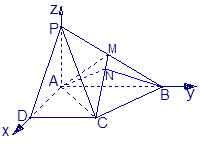
,∴以A为坐标原点如图建立空间直角坐标系,取
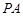 的中点
的中点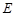 ,
,则各点坐标为:
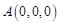 ,
,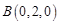 ,
, ,
,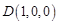 ,
,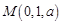 ,
,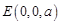 ;
;∴
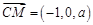 ,
,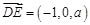 ,∴
,∴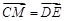 ,∴
,∴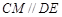 ,∴
,∴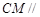 平面
平面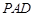 ;
;⑵由
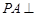 底面
底面 及
及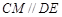 ,得
,得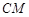 与平面
与平面 所成角的大小为
所成角的大小为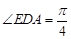 ;
;∴
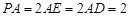 ,∴
,∴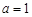 ,
,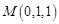 ,
,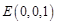 ,
,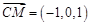 ;
;取
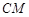 的中点
的中点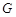 ,则因
,则因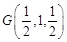 ,
,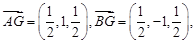 ∴
∴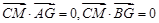 ;
;则
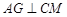 ,且
,且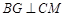 ,∴
,∴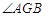 为二面角
为二面角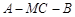 的平面角;
的平面角;∵
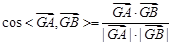
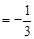 ;∴二面角
;∴二面角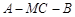 的余弦值
的余弦值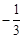

练习册系列答案
相关题目
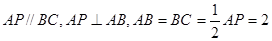 ,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP
,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP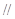 平面EFG;(2)当二面角G-EF-D的大小为
平面EFG;(2)当二面角G-EF-D的大小为 时,求FG与平面PBC所成角的余弦值.
时,求FG与平面PBC所成角的余弦值.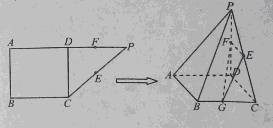
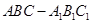 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是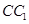 棱的中点,AE交
棱的中点,AE交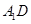 于点H.
于点H.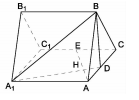
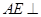 平面
平面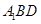 ;
;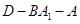 的余弦值;
的余弦值;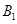 到平面
到平面 D,使得平面BC
D,使得平面BC 平面ABD.
平面ABD.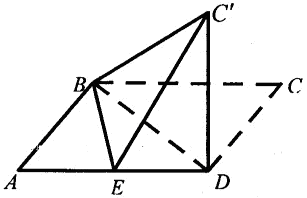
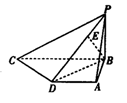
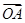 =a,
=a,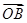 =b,
=b,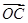 =c,用a,b,c表示向量
=c,用a,b,c表示向量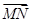 =________.
=________.