题目内容

已知f（2x）=6x-1，则f（x）=
 
．
考点：函数解析式的求解及常用方法
专题：计算题
分析：利用配凑法或者换元法求解该类函数的解析式，注意复合函数中的自变量与简单函数自变量之间的联系与区别．
解答： 解：由f（2x）=6x-1，
得到f（2x）=3（2x-
1
3
）=3（2x）-1
故f（x）=3x-1
故答案为：3x-1．
点评：本题考查函数解析式的求解，考查学生的整体意识和换元法的思想．
练习册系列答案
相关题目
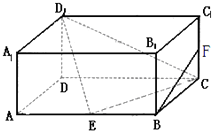如图，在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，E为AB的中点，F为CC1的中点．
（1）证明：BF∥平面ECD1；
（2）求二面角D1-EC-D的余弦值．
若直线y=k（x-2）与函数y=x2+2x的图象交于点（-1，-1），则两图象一共有
 
个交点．
函数y=1+log
1
2
x在x∈[2，8]的值域
 
．
已知球的直径PQ=4，A、B、C是该球球面上的三点，∠APQ=∠BPQ=∠CPQ=30°，△ABC是正三角形，则棱锥P-ABC的体积为
 
．
已知集合A={1，-1}，B={-1，a}，且A=B，则实数a=
 
．
如果关于x的不等式|x-a|+|x+4|≥1的解集是全体实数，则实数a的取值范围是
 
．
△ABC中，sinA=
5
5
，sinB=
10
10
，则
b
a
=
 
．
参数方程
x=1+cosθ
y=-2+sinθ
（θ为参数）所表示的图形是（　　）
A、直线B、射线C、圆D、半圆

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网