题目内容
四棱锥![]() 的底面为正方形,
的底面为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为
为![]() 上的点.
上的点.
(1)求证:无论点![]() 在
在![]() 上如何移动,都有
上如何移动,都有![]() ;
;
(2)若![]() //平面
//平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
(1)见解析(2)![]()
解析:
(1)证明:以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴的正半轴建立如图所示的空间坐标系,
轴的正半轴建立如图所示的空间坐标系,
设![]() ,
,
则![]() ,
,![]()
![]() ,
,![]()
![]()
![]() 无论点
无论点![]() 在
在![]() 上如何移动,都有
上如何移动,都有![]()
(2)连接![]() ,设
,设![]() ,连接
,连接![]() .
.
![]()
![]() //平面
//平面![]() ,平面
,平面![]() 平面
平面![]()
![]()
![]() //
//![]() ,
,
![]()
![]() 是
是![]() 的中点,
的中点,![]()
![]() 是
是![]() 的中点,
的中点,![]()
![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则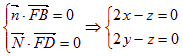 ,
,
取![]() ,得
,得![]() ,易知平面
,易知平面![]() 的法向量为
的法向量为![]()
![]()
 ,
,
设二面角![]() 的平面角为
的平面角为![]() ,依题知
,依题知![]() ,
,![]()
![]() .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为h1,h2,h,则h1:h2:h=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )
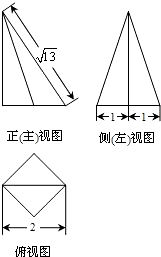

| A、1 | B、2 | C、3 | D、4 |
一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )


| A、1 | B、2 | C、3 | D、4 |
 (2012•贵溪市模拟)如图,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积
(2012•贵溪市模拟)如图,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积