题目内容
(满分12分)设底面边长为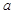 的正四棱柱
的正四棱柱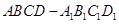 中,
中,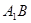 与平面
与平面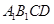 所成角为
所成角为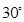 ;点
;点 是棱
是棱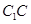 上一点.
上一点.
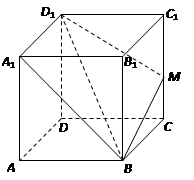
(1)求证:正四棱柱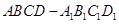 是正方体;
是正方体;
(2)若点 在棱
在棱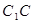 上滑动,求点
上滑动,求点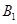 到平面
到平面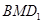 距离的最大值;
距离的最大值;
(3)在(2)的条件下,求二面角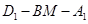 的大小.
的大小.
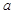 的正四棱柱
的正四棱柱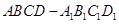 中,
中,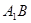 与平面
与平面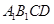 所成角为
所成角为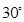 ;点
;点 是棱
是棱 上一点.
上一点.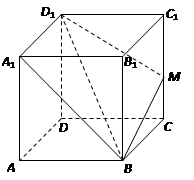
(1)求证:正四棱柱
 是正方体;
是正方体;(2)若点
 在棱
在棱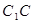 上滑动,求点
上滑动,求点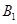 到平面
到平面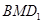 距离的最大值;
距离的最大值;(3)在(2)的条件下,求二面角
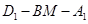 的大小.
的大小.(1).证明:见解析;(2)点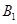 到平面
到平面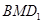 的最大距离是
的最大距离是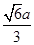 ;(3)
;(3)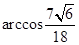 .
.
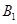 到平面
到平面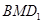 的最大距离是
的最大距离是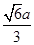 ;(3)
;(3)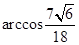 .
.本试题主要考查了立体几何中正方体概念,和点到面的距离的最值和二面角的求解和运算的综合试题。
(1)利用正四棱柱的性质,加上题目中的边的关系,结合概念得到。
(2)对于点到面的距离关键是找到平面的垂线,利用面面垂直的性质定理得到点到面的距离的表示,从而求解最值。
(3)建立合理的空间直角坐标系,然后设出法向量来表示二面角的平面角的大小来解决。
(1).证明:设正四棱柱的侧棱长为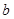 ,作
,作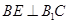 与
与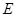 ,连接
,连接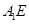 ,
,
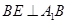 ,
,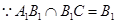 ,
, ,
,
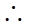
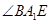 是
是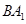 与
与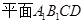 所成的角,
所成的角,
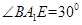
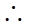
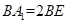 ,即
,即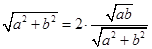
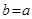
所以四棱柱正四棱柱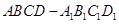 是正方体;......................4'
是正方体;......................4'
(2).设点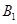 到平面
到平面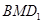 的距离为
的距离为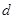 ,
,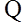
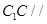 平面
平面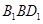 ,
,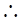 点
点 、
、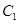 到平面
到平面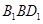 的距离相等为
的距离相等为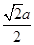 .在四面体
.在四面体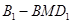 中,体积
中,体积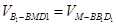 ,
,
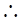
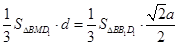
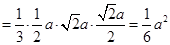
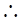
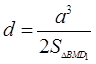 ,设
,设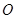 是
是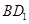 中点,当
中点,当 也是棱
也是棱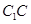 中点时,
中点时,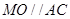 ,有
,有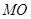
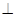 平面
平面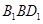 ,
,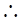
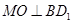 于
于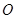 ,
,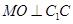 于
于 ,
,
 是一面直线
是一面直线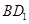 和
和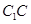 的公垂线段,
的公垂线段,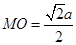 是
是 到直线
到直线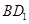 的最短距离,
的最短距离,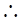
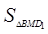 的最小值是
的最小值是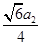
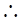
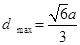 ,即点
,即点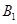 到平面
到平面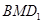 的最大距离是
的最大距离是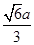 .....................8'
.....................8'
(3).以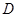 为原点,
为原点,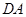 、
、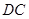 、
、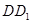 分别为
分别为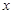 、
、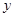 、
、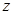 轴建立平面直角坐标系,由(2)知
轴建立平面直角坐标系,由(2)知 也是棱
也是棱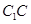 中点,则
中点,则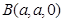 、
、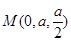 、
、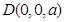 、
、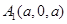 ,设平面
,设平面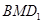 的法向量
的法向量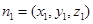 ,平面
,平面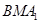 的法向量
的法向量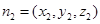 由
由
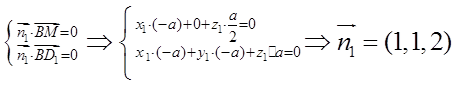 ;
;
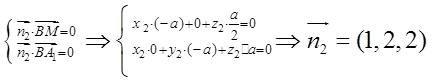 。
。
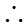
 面角
面角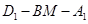 的大小是
的大小是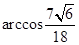 .............................12'
.............................12'
(1)利用正四棱柱的性质,加上题目中的边的关系,结合概念得到。
(2)对于点到面的距离关键是找到平面的垂线,利用面面垂直的性质定理得到点到面的距离的表示,从而求解最值。
(3)建立合理的空间直角坐标系,然后设出法向量来表示二面角的平面角的大小来解决。
(1).证明:设正四棱柱的侧棱长为
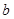 ,作
,作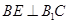 与
与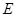 ,连接
,连接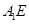 ,
,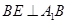 ,
,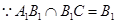 ,
, ,
,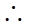
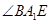 是
是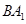 与
与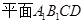 所成的角,
所成的角,
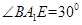
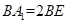 ,即
,即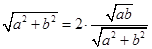
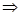
所以四棱柱正四棱柱
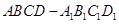 是正方体;......................4'
是正方体;......................4'(2).设点
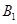 到平面
到平面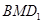 的距离为
的距离为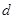 ,
,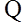
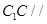 平面
平面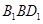 ,
,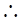 点
点 、
、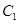 到平面
到平面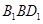 的距离相等为
的距离相等为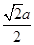 .在四面体
.在四面体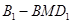 中,体积
中,体积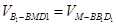 ,
,
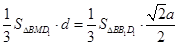
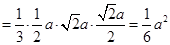
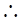
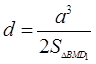 ,设
,设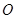 是
是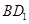 中点,当
中点,当 也是棱
也是棱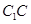 中点时,
中点时,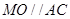 ,有
,有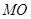
 平面
平面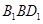 ,
,
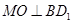 于
于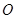 ,
,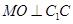 于
于 ,
,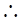
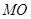 是一面直线
是一面直线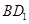 和
和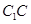 的公垂线段,
的公垂线段,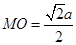 是
是 到直线
到直线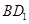 的最短距离,
的最短距离,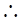
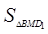 的最小值是
的最小值是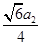
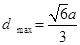 ,即点
,即点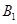 到平面
到平面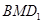 的最大距离是
的最大距离是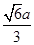 .....................8'
.....................8'(3).以
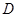 为原点,
为原点,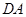 、
、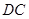 、
、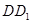 分别为
分别为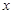 、
、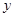 、
、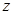 轴建立平面直角坐标系,由(2)知
轴建立平面直角坐标系,由(2)知 也是棱
也是棱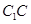 中点,则
中点,则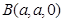 、
、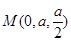 、
、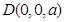 、
、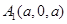 ,设平面
,设平面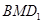 的法向量
的法向量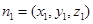 ,平面
,平面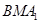 的法向量
的法向量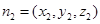 由
由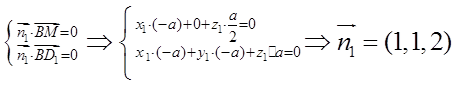 ;
;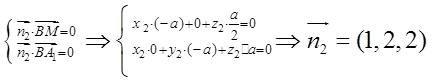 。
。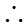
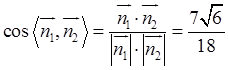
 面角
面角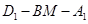 的大小是
的大小是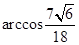 .............................12'
.............................12'
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 a(0<
a(0<
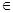 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE: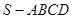 中,底面
中,底面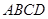 是直角梯形,
是直角梯形,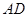 ∥
∥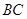 ,
,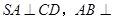 平面
平面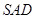 ,点
,点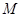 是
是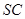 的中点,且
的中点,且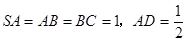 .
.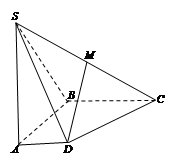
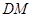 ∥平面
∥平面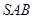 ;
;
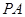 ∥平面
∥平面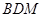 ;
;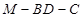 的余弦值。
的余弦值。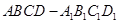 中,
中,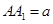 ,
,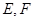 分别是
分别是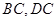 的中点,则异面直线
的中点,则异面直线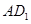 与
与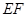 所成角为
所成角为
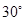
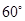
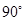
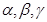 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: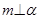 ,
,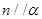 ,则
,则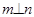 ②若
②若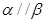 ,
,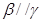 ,
,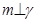
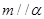 ,
,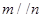 ④若
④若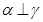 ,
,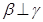 ,则
,则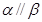
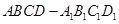 是正方体,点
是正方体,点 为正方体对角线的交点,过点
为正方体对角线的交点,过点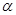 ,正方体的八个顶点到平面
,正方体的八个顶点到平面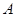 的元素,则集合
的元素,则集合