题目内容
(本小题满分9分) 如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE= a(0<
a(0< ≦1).
≦1).
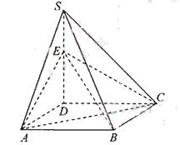
(Ⅰ)求证:对任意的
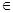 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求 的值。
的值。
 a(0<
a(0< ≦1).
≦1). 
(Ⅰ)求证:对任意的

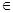 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:(Ⅱ)若二面角C-AE-D的大小为600C,求
 的值。
的值。(Ⅰ)见解析;(II) 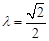 。
。
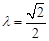 。
。运用三垂线定理证明线线垂直,第二问是告诉二面角求参数的值,这是二面角的逆向问题,仍然要作出二面角,求二面角才能解出参数。这题除了用传统的证法与求角的方法外,也可以应用空间向量来解决。
解:(Ⅰ)证发1:连接BD,由底面是正方形可得AC BD。
BD。
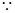 SD
SD 平面ABCD,
平面ABCD,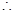 BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影,
由三垂线定理得AC BE.
BE.
(II)解法1: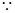 SD
SD 平面ABCD,CD
平面ABCD,CD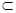 平面ABCD,
平面ABCD,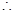 SD
SD CD.
CD.
又底面ABCD是正方形,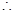 CD
CD AD,又SD
AD,又SD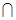 AD=D,
AD=D,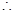 CD
CD 平面SAD。
平面SAD。
过点D在平面SAD内做DF AE于F,连接CF,则CF
AE于F,连接CF,则CF AE,
AE,
故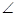 CFD是二面角C-AE-D 的平面角,即
CFD是二面角C-AE-D 的平面角,即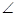 CFD=60°
CFD=60°
在Rt△ADE中,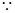 AD=
AD=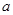 , DE=
, DE= 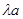 , AE=
, AE=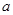
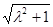 。
。
于是,DF=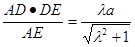
在Rt△CDF中,由 cot60°=
cot60°=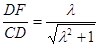
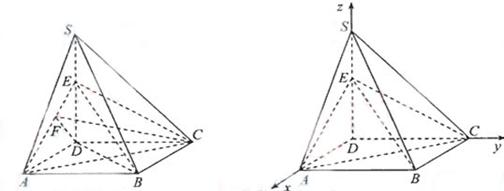
得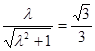 , 即
, 即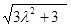 =3
=3 解得
解得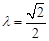 。
。
解:(Ⅰ)证发1:连接BD,由底面是正方形可得AC
 BD。
BD。 SD
SD 平面ABCD,
平面ABCD, BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影,由三垂线定理得AC
 BE.
BE.(II)解法1:
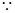 SD
SD 平面ABCD,CD
平面ABCD,CD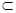 平面ABCD,
平面ABCD,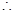 SD
SD CD.
CD. 又底面ABCD是正方形,
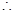 CD
CD AD,又SD
AD,又SD AD=D,
AD=D, CD
CD 平面SAD。
平面SAD。过点D在平面SAD内做DF
 AE于F,连接CF,则CF
AE于F,连接CF,则CF AE,
AE, 故
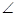 CFD是二面角C-AE-D 的平面角,即
CFD是二面角C-AE-D 的平面角,即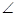 CFD=60°
CFD=60° 在Rt△ADE中,
 AD=
AD=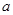 , DE=
, DE= 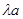 , AE=
, AE=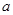
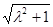 。
。于是,DF=
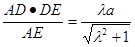
在Rt△CDF中,由
 cot60°=
cot60°=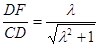

得
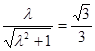 , 即
, 即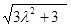 =3
=3 解得
解得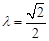 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 矩形ABCD所在的平面,M,N分别为AB,PC的中点。求证:
矩形ABCD所在的平面,M,N分别为AB,PC的中点。求证: 平面
平面


 面ABCD,E为AB中点,求证:面
面ABCD,E为AB中点,求证:面 面
面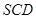
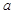 的正四棱柱
的正四棱柱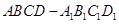 中,
中,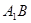 与平面
与平面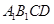 所成角为
所成角为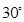 ;点
;点 是棱
是棱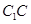 上一点.
上一点.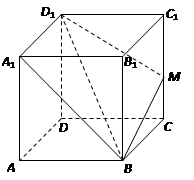
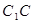 上滑动,求点
上滑动,求点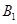 到平面
到平面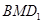 距离的最大值;
距离的最大值;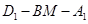 的大小.
的大小.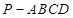 中,
中,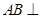 平面
平面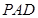 ,
,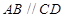 ,
,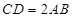 ,
,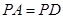 ,
,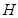 是
是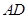 的中点.
的中点.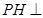 平面
平面 ;
;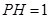 ,
,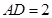 ,
,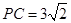 ,求二面角
,求二面角 的正切值.
的正切值.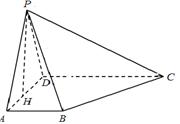
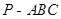 各侧棱长均为
各侧棱长均为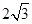 ,三个顶角均为
,三个顶角均为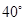 ,M,N分别为PA,PC上的点,求
,M,N分别为PA,PC上的点,求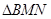 周长的最小值.
周长的最小值.




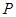 在正方体
在正方体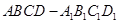 的面对角线
的面对角线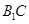 上运动,
上运动,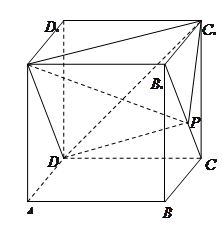

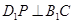 ;
;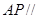 平面
平面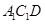 ;
;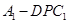 的体积随点
的体积随点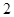 的正方体
的正方体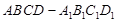 中,点
中,点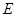 ,
,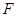 分别是棱
分别是棱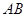 ,
,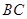 的中点,则点
的中点,则点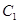 到平面
到平面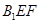 的距离是( ).
的距离是( ).


