题目内容
设a是实数,函数f(x)=ax2+2(a-1)x-2lnx.
(Ⅰ)讨论函数f(x)的单调区间;
(Ⅱ)设定义在D上的函数y=g(x)在点P(x0,y0)处的切线方程为l:y=h(x),当x≠x0时,若
<0在D内恒成立,则称点P为函数y=g(x)的“平衡点”.当a=1时,试问函数y=f(x)是否存在“平衡点”?若存在,请求出“平衡点”的横坐标;若不存在,请说明理由.
(Ⅰ)讨论函数f(x)的单调区间;
(Ⅱ)设定义在D上的函数y=g(x)在点P(x0,y0)处的切线方程为l:y=h(x),当x≠x0时,若
| g(x)-h(x) |
| x-x0 |
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:函数的性质及应用
分析:(1)先求导,f′(x)=2ax+2(a-1)-
=
(x>0),分当a≤0时,与a>0时,讨论导数的符号,得出单调区间;
(2)设p(x0,y0)为函数f(x)=x2-2lnx图象上一点,则函数y=f(x)在点P处的切线方程为:y-x02+2lnx0=(2x0-
)(x-x0)得h(x)的表达式,
构造函数F(x)=f(x)-h(x)=x2-2lnx-(2x0x-x02-
+2-2lnx0),求导研究F(x)的单调性,再验证
<0是否恒成立.
| 2 |
| x |
| (2ax-2)(x+1) |
| x |
(2)设p(x0,y0)为函数f(x)=x2-2lnx图象上一点,则函数y=f(x)在点P处的切线方程为:y-x02+2lnx0=(2x0-
| 2 |
| x0 |
构造函数F(x)=f(x)-h(x)=x2-2lnx-(2x0x-x02-
| 2x |
| x0 |
| g(x)-h(x) |
| x-x0 |
解答:
解:(1)f′(x)=2ax+2(a-1)-
=
(x>0)
当a≤0时,f′(x)≤0在x>0上恒成立;
当a>0时,在x∈(0,
)时,f′(x)<0,当x∈(
,+∞)时,f′(x)>0
所以,当a≤0时,f(x)的减区间为(0,+∞);
当a>0时,f(x)的减区间为(0,
),增区间为(
,+∞).
(2)设p(x0,y0)为函数f(x)=x2-2lnx图象上一点,则函数y=f(x)在点P处的切线方程为:y-x02+2lnx0=(2x0-
)(x-x0)
即:h(x)=2x0x-x02-
+2-2lnx0.
令F(x)=f(x)-h(x)=x2-2lnx-(2x0x-x02-
+2-2lnx0).
则F′(x)=2x-
-2x0+
=2(x-x0)(1+
),
因为x>0,x0>0
所以,当0<x<x0时,F′(x)<0,当x>x0时,F′(x)>0
即函数F(x)在(0,x0)上为减函数,在(x0,+∞)上为增函数,
所以,F(x)≥F(x0)=0
那么,当x<x0时,
=
<0;
当x>x0时,
=
>0;
因此,函数f(x)在x∈(0,+∞)不存在“平衡点”.
| 2 |
| x |
| (2ax-2)(x+1) |
| x |
当a≤0时,f′(x)≤0在x>0上恒成立;
当a>0时,在x∈(0,
| 1 |
| a |
| 1 |
| a |
所以,当a≤0时,f(x)的减区间为(0,+∞);
当a>0时,f(x)的减区间为(0,
| 1 |
| a |
| 1 |
| a |
(2)设p(x0,y0)为函数f(x)=x2-2lnx图象上一点,则函数y=f(x)在点P处的切线方程为:y-x02+2lnx0=(2x0-
| 2 |
| x0 |
即:h(x)=2x0x-x02-
| 2x |
| x0 |
令F(x)=f(x)-h(x)=x2-2lnx-(2x0x-x02-
| 2x |
| x0 |
则F′(x)=2x-
| 2 |
| x |
| 2 |
| x0 |
| 1 |
| x0x |
因为x>0,x0>0
所以,当0<x<x0时,F′(x)<0,当x>x0时,F′(x)>0
即函数F(x)在(0,x0)上为减函数,在(x0,+∞)上为增函数,
所以,F(x)≥F(x0)=0
那么,当x<x0时,
| F(x) |
| x-x0 |
| f(x)-h(x) |
| x-x0 |
当x>x0时,
| F(x) |
| x-x0 |
| f(x)-h(x) |
| x-x0 |
因此,函数f(x)在x∈(0,+∞)不存在“平衡点”.
点评:本题主要考查函数的性质,研究函数的导数与函数的关系,对于题目出现新定义的问题,读懂定义的内涵是关键.

练习册系列答案
相关题目
设f(x)是R上的偶函数,且在[0,+∞)上是增函数,又f(1)=0,则满足f(log2x)>0的x的取值范围是( )
| A、(2,+∞) | ||
B、(0,
| ||
C、(0,
| ||
D、(
|
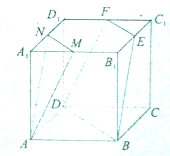 棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.
棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.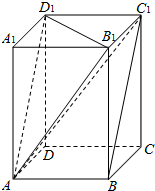 如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,异面直线AD与BC1所成角的大小为60°,求:
如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,异面直线AD与BC1所成角的大小为60°,求: