题目内容
5.已知函数f(x)=4x+3sinx,x∈(-1,1),如果f(1-a)+f(1-a2)<0成立,则实数a的取值范围为(1,$\sqrt{2}$).分析 利用导数判断函数的单调性,然后判断函数的奇偶性,化简不等式,得到不等式组求解即可.
解答 解:函数f(x)=4x+3sinx,x∈(-1,1),
满足f(-x)=-(4x+3sinx)=-f(x),函数是奇函数.
f′(x)=4+3cosx,x∈(-1,1),f′(x)>0.
函数是增函数,
f(1-a)+f(1-a2)<0成立,
可得f(1-a)<f(a2-1)成立,
可得$\left\{\begin{array}{l}-1<1-a\\ 1-a<{a}^{2}-1\\{a}^{2}-1<1\end{array}\right.$,
解得:a∈(1,$\sqrt{2}$).
故答案为:(1,$\sqrt{2}$).
点评 本题考查函数的导数与函数的单调性的关系,函数的奇偶性的应用,考查函数与方程的思想以及计算能力.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
15.方程xy2-x2y=8x所表示的曲线( )
| A. | 关于y轴对称 | B. | 关于y+x=0对称 | C. | 关于原点对称 | D. | 关于x-y=0对称 |
16.某个几何体的三视图如图所示,则该几何体的体积是( )
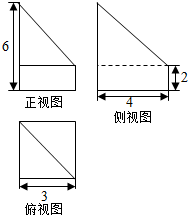

| A. | 30 | B. | 40 | C. | 24 | D. | 72 |
13.如果两圆的方程是x2+y2=4和x2+y2-6x-8y+9=0,那么这两个圆的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |