题目内容
16．某个几何体的三视图如图所示，则该几何体的体积是（ ）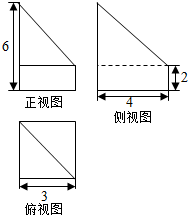
| A． | 30 | B． | 40 | C． | 24 | D． | 72 |
分析 根据几何体的三视图，得出该几何体是长方体与四棱锥的组合体，根据图中数据求出它的体积即可．
解答 解：根据几何体的三视图，得；
该几何体是下部为长方体，上部为四棱锥的组合体，
如图所示；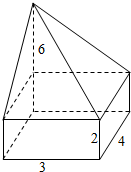
所以，该几何体的体积为
V=V四棱锥+V长方体=$\frac{1}{3}$×3×4×（6-2）+3×4×2=40．
故选：B．
点评 本题考查了空间几何体的三视图的应用问题，解题的关键是根据三视图还原出几何体的结构特征，是基础题目．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
6．已知实数x、y满足$\left\{\begin{array}{l}{x+y≥2}\\{x-y≤2}\\{0≤y≤3}\end{array}\right.$，则z=2x-y的取值范围是（ ）
| A． | [-5，7] | B． | [5，7] | C． | [4，7] | D． | [-5，4] |
7．过抛物线y2=4x的焦点F作倾斜角为60°的直线，交抛物线于A，B两点（A在x轴上方），那么$\frac{{|{AF}|}}{{|{BF}|}}$=（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{2}$ | C． | 3 | D． | 2 |
4．A、B两人约定在星期天上午在紫阳公园会面，并约定先到者须等候一刻钟，过时即可离去；若A是6点半到达，假设B在6点到7点之间的任何时刻到达是等可能的，则两人能会面的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
11．函数y=x2+2x-3，定义域为（-3，4），则此函数值域为（ ）
| A． | （-1，20） | B． | [-1，20] | C． | [-4，21） | D． | （-5，20） |
1．某四棱锥的三视图如图所示，该四棱锥的表面积是（ ）
| A． | 16$\sqrt{2}$ | B． | 16+16$\sqrt{2}$ | C． | 32$\sqrt{2}$ | D． | 16+32$\sqrt{2}$ |
6．一个质量均匀的骰子（六个点数），若连续投掷三次，取三次的点数分别作为三角形的边长，则其能构成钝角三角形的概率为（ ）
| A． | $\frac{13}{72}$ | B． | $\frac{1}{27}$ | C． | $\frac{31}{72}$ | D． | $\frac{4}{27}$ |