题目内容
14.($\sqrt{x}$+$\frac{1}{x}$)n的展开式中只有第六项的二项式系数最大,则第四项为120$\sqrt{x}$.分析 由条件求得n=10,再利用二项展开式的通项公式求得它的第四项.
解答 解:($\sqrt{x}$+$\frac{1}{x}$)n的展开式中只有第六项的二项式系数最大,则n=10,
故第四项为 ${C}_{10}^{3}$•$\sqrt{x}$=120$\sqrt{x}$,
故答案为:120$\sqrt{x}$.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
3.如果经计算得到事件A和事件B无关,那么( )
| A. | x2>6.635 | B. | x2≤6.635 | C. | x2≤3.841 | D. | x2>3.841 |
4.在正项等比数列{an}中,a1=2,S3=$\frac{26}{9}$,则数列{an}的通项公式为( )
| A. | 2×($\frac{2}{3}$)n-1 | B. | 2×($\frac{1}{3}$)n-1 | C. | 2×($\frac{4}{3}$)n-1 | D. | 2×($\frac{4}{3}$)n |
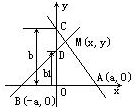 如图,二杆各绕点A(a,0)和B(-a,0)旋转,且它们在y轴上的截距的乘积bb1=a2(常数),试求旋转杆交点的轨迹方程.
如图,二杆各绕点A(a,0)和B(-a,0)旋转,且它们在y轴上的截距的乘积bb1=a2(常数),试求旋转杆交点的轨迹方程.