题目内容

4．在平面直角坐标系中，过动点P分别作圆C1：x2+y2-4x-6y+9=0与圆C2：x2+y2+2x+2y+1=0的切线PA与PB（A，B为切点），若|PA|=|PB|若O为原点，则|OP|的最小值为（　　）
A．2B．$\frac{4}{5}$C．$\frac{3}{5}$D．$\sqrt{5}$

分析 利用|PA|=|PB|，结合勾股定理，即可求得点P的轨迹方程，|OP|的最小值为O到直线的距离．

解答 解：设P（x，y），则
∵|PA|=|PB|，
∴x2+y2-4x-6y+9=x2+y2+2x+2y+1，
∴3x+4y-4=0，
∴|OP|的最小值为O到直线的距离，即$\frac{|-4|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{4}{5}$
故选：B．

点评 本题考查点P的轨迹方程，考查点到直线的距离公式，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
19．若函数f（x）定义域内有两个任意实数x1，x2（x1≠x2），若$f（\frac{{{x_1}+{x_2}}}{2}）$＜$\frac{{f（{x_1}）+f（{x_2}）}}{2}$恒成立，则称为f（x）凹函数；若满足$f（\frac{{{x_1}+{x_2}}}{2}）$＞$\frac{{f（{x_1}）+f（{x_2}）}}{2}$恒成立，则称函数f（x）为凸函数，试证明：任一指数函数f（x）=ax（a＞0，a≠1）都是凹函数．
15．如图，一个平面图形的斜二测画法的直观图是一个边长为a的正方形，则原平面图形的面积为（　　）
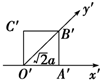
A．$\frac{\sqrt{2}}{4}$a2B．a2C．2$\sqrt{2}$a2D．2a2
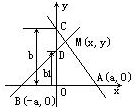12．已知x+x-1=2，求$\frac{{x}^{2}+{x}^{-2}-2}{{x}^{\frac{3}{2}}+{x}^{-\frac{3}{2}}-3}$．
19．已知mx2-3x+1=0有且只有一个实根在区间（0，1）内，求实数m的取值范围．
9．如图，二杆各绕点A（a，0）和B（-a，0）旋转，且它们在y轴上的截距的乘积bb1=a2（常数），试求旋转杆交点的轨迹方程．
16．求方程组$\left\{\begin{array}{l}{x\sqrt{yz}+y\sqrt{xz}=39-xy}\\{y\sqrt{xz}+z\sqrt{xy}=52-yz}\\{z\sqrt{xy}+x\sqrt{yz}=78-xz}\end{array}\right.$的正数解．
13．已知a，b∈R+．
（1）求证：$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{a}$≥a+b；
（2）利用（1）的结论，求函数y=$\frac{{{{（1-x）}^2}}}{x}+\frac{x^2}{1-x}$（0＜x＜1）的最小值．
14．已知|$\overrightarrow{a}$|=10，|$\overrightarrow{b}$|=12，且$\overrightarrow{a}$•（$\frac{1}{2}$$\overrightarrow{b}$）=-30，则$\overrightarrow{a}$和$\overrightarrow{b}$的夹角为（　　）
A．60°B．120°C．135°D．150°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网