题目内容
4.若函数f(x)=2sin(ωx+φ)的图象(部分)如图所示,则ω和φ的可能取值是( )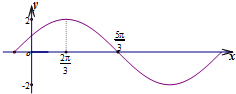
| A. | ω=1,φ=$\frac{π}{3}$ | B. | ω=1,φ=-$\frac{π}{3}$ | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{6}$ | D. | ω=$\frac{1}{2}$,φ=-$\frac{π}{6}$ |
分析 由周期求出ω,由五点法作图求出φ的值,可得结论.
解答 解:根据函数f(x)=2sin(ωx+φ)的图象(部分),
可得$\frac{T}{4}$=$\frac{1}{4}•\frac{2π}{ω}$=$\frac{5π}{3}$-$\frac{2π}{3}$=π,∴ω=$\frac{1}{2}$.
再根据五点法作图可得$\frac{1}{2}•\frac{2π}{3}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{6}$,
故选:C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
14.(ax+$\frac{1}{x}$+y)6的展开式中,x2y2的系数为-480,则a=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
9.sin600°的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |

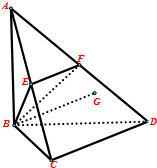 如图:AB⊥面BCD,BC=CD,∠BCD=90°.∠ADB=30°,E,F分别是AC,AD的中点.
如图:AB⊥面BCD,BC=CD,∠BCD=90°.∠ADB=30°,E,F分别是AC,AD的中点.