题目内容
已知函数f(x)=ex-1-ax(a∈R).
(1)求函数f(x)的单调区间;
(2)当x∈(0,2]时,讨论函数F(x)=f(x)-xlnx零点的个数;
(3)若g(x)=ln(ex-1)-lnx,当0<a≤1时,求证:f[g(x)]<f(x).
(1)求函数f(x)的单调区间;
(2)当x∈(0,2]时,讨论函数F(x)=f(x)-xlnx零点的个数;
(3)若g(x)=ln(ex-1)-lnx,当0<a≤1时,求证:f[g(x)]<f(x).
考点:导数在最大值、最小值问题中的应用,根的存在性及根的个数判断,利用导数研究函数的单调性
专题:计算题,证明题,分类讨论,函数的性质及应用,导数的综合应用
分析:(1)求函数f(x)的导数,对a讨论,分当a≤0时,当a>0时,令导数大于0,得增区间,令导数小于0,得减区间;
(2)对F(x)=f(x)-xlnx进行化简,构造函数h(x)=
-xlnx(x>0),研究函数h(x)的单调性和最值,即可确定F(x)=f(x)-xlnx在定义域内是否存在零点;
(3)由(1)知,当0<a≤1时,f(x)在(0,+∞)上单调递增,要证明f(g(x))<f(x),只要证明g(x)<x即可.
(2)对F(x)=f(x)-xlnx进行化简,构造函数h(x)=
| ex-1 |
| x |
(3)由(1)知,当0<a≤1时,f(x)在(0,+∞)上单调递增,要证明f(g(x))<f(x),只要证明g(x)<x即可.
解答:
解:(1)函数的定义域为(-∞,+∞),
f′(x)=(ex-ax-1)′=ex-a.
当a≤0时,f′(x)>0恒成立,即有f(x)在R上递增;
当a>0时,由f′(x)<0,得ex-a<0,ex<a,∴x<lna,
由f′(x)>0,得ex-a>0,ex>a,∴x>lna,
所以函数的单调减区间为(-∞,lna),单调增区间是(lna,+∞).
(2)函数F(x)=f(x)-xlnx的定义域为(0,+∞),
由F(x)=0,得a=
-lnx(x>0),
令h(x)=
-lnx(x>0),
则h′(x)=
,
由于x>0,ex-1>0,可知当x>1,h′(x)>0;当0<x<1时,h′(x)<0,
故函数h(x)在(0,1)上单调递减,在(1,2]上单调递增,故h(x)≥h(1)=e-1.
又h(2)=
当a=1时,对?x>0,有f(x)>f(lna)=0,即ex-1>x,即
>1,
当e-1<a<
<e-1时,函数F(x)有两个不同的零点;
当a=e-1或a=
时,函数F(x)有且仅有一个零点;
当a<e-1或a
时,函数F(x)没有零点;
(3)由(1)知,当0<a≤1时f(x)在(0,+∞)上单调递增,且f(0)=0;
∴对x>0时,有f(x)>0,则ex-1>ax;
故对任意x>0,ln(ex-1)-ln(ax)>g(x)=ln(ex-1)-lnx>0;
所以,要证f[g(x)]<f(x),只需证:?x>0,g(x)<x;
只需证:?x>0,ln(ex-1)-lnx<x;即证:ln(ex-1)<lnx+lnex;
即证:?x>0,xex>ex-1; 所以,只要证:?x>0,xex-ex+1>0,
令H(x)=xex-ex+1,则H′(x)=xex>0,
故函数H(x)在(0,+∞)上单调递增.∴H(x)>H(0)=0;
∴对?x>0,xex-ex+1>0成立,即g(x)<x,
∴f[g(x)]<f(x).
f′(x)=(ex-ax-1)′=ex-a.
当a≤0时,f′(x)>0恒成立,即有f(x)在R上递增;
当a>0时,由f′(x)<0,得ex-a<0,ex<a,∴x<lna,
由f′(x)>0,得ex-a>0,ex>a,∴x>lna,
所以函数的单调减区间为(-∞,lna),单调增区间是(lna,+∞).
(2)函数F(x)=f(x)-xlnx的定义域为(0,+∞),
由F(x)=0,得a=
| ex-1 |
| x |
令h(x)=
| ex-1 |
| x |
则h′(x)=
| (ex-1)(x-1) |
| x2 |
由于x>0,ex-1>0,可知当x>1,h′(x)>0;当0<x<1时,h′(x)<0,
故函数h(x)在(0,1)上单调递减,在(1,2]上单调递增,故h(x)≥h(1)=e-1.
又h(2)=
| e2-1 |
| 4 |
当a=1时,对?x>0,有f(x)>f(lna)=0,即ex-1>x,即
| ex-1 |
| x |
当e-1<a<
| e2-1 |
| 4 |
当a=e-1或a=
| e2-1 |
| 4 |
当a<e-1或a
| e2-1 |
| 4 |
(3)由(1)知,当0<a≤1时f(x)在(0,+∞)上单调递增,且f(0)=0;
∴对x>0时,有f(x)>0,则ex-1>ax;
故对任意x>0,ln(ex-1)-ln(ax)>g(x)=ln(ex-1)-lnx>0;
所以,要证f[g(x)]<f(x),只需证:?x>0,g(x)<x;
只需证:?x>0,ln(ex-1)-lnx<x;即证:ln(ex-1)<lnx+lnex;
即证:?x>0,xex>ex-1; 所以,只要证:?x>0,xex-ex+1>0,
令H(x)=xex-ex+1,则H′(x)=xex>0,
故函数H(x)在(0,+∞)上单调递增.∴H(x)>H(0)=0;
∴对?x>0,xex-ex+1>0成立,即g(x)<x,
∴f[g(x)]<f(x).
点评:本题以函数为载体,主要考查导数的几何意义,考查导数在研究函数的单调性和最值中的应用,考查恒成立问题的解决方法,属于中档题.

练习册系列答案
相关题目
三角形三边长为a,b,c,且满足关系式(a+b+c)(a+b-c)=3ab,则c边的对角等于( )
| A、15° | B、45° |
| C、60° | D、120° |
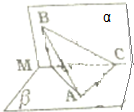 在直二面角α-MN-β中,等腰直角△ABC的斜边BC?α,一直角边AC?β,BC与β所成角的正弦值为
在直二面角α-MN-β中,等腰直角△ABC的斜边BC?α,一直角边AC?β,BC与β所成角的正弦值为
| ||
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|