题目内容
已知数列{an}满足a1=1，且anan+1=2n，则数列{an}的前20项的和为（ ）
| A、3×211-3 |
| B、3×211-1 |
| C、3×210-2 |
| D、3×210-5 |
考点：数列的求和,数列递推式
专题：等差数列与等比数列
分析：由已知得数列{an}的奇数项是首项为1，公比为2的等比数列，偶数项是首项为2，公比为2的等比数列，由此能求出前20项的和．
解答：
解：∵数列{an}满足a1=1，且anan+1=2n，
∴a2=
=2，an-1an=2n-1，n≥2，
∴
=
=2，
∴则数列{an}的奇数项是首项为1，公比为2的等比数列，
偶数项是首项为2，公比为2的等比数列，
∴前20项的和为：
S20=
+
=3×210-5．
故选：D．
∴a2=
| 2 |
| 1 |
∴
| anan+1 |
| an-1an |
| an+1 |
| an-1 |
∴则数列{an}的奇数项是首项为1，公比为2的等比数列，
偶数项是首项为2，公比为2的等比数列，
∴前20项的和为：
S20=
| 1-210 |
| 1-2 |
| 2(2-210) |
| 1-2 |
故选：D．
点评：本题考查数列的前20项的和的求法，是中档题，解题时要认真审题，解题的关键是推导出数列{an}的奇数项是首项为1，公比为2的等比数列，偶数项是首项为2，公比为2的等比数列．
练习册系列答案
相关题目
当输入的实数x∈[2，30]时，执行如图所示的程序框图，则输出的x不小于103的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
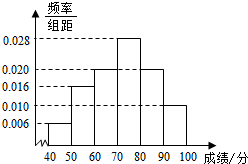某校高三文科（1）班学生参加“江南十校”联考，其数学成绩（已折合成百分制）的频率分布直方图如图所示，其中成绩分布敬意为[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]，现已知成绩落在[90，100]的有5人．