题目内容

已知函数f（x）=x|x-4|，则不等式f（x）≥f（1）的解集为
 
．
考点：绝对值不等式的解法
专题：计算题,推理和证明
分析：f（x）=x|x-4|=
(x-2)2-4，x≥4
-(x-2)2+4，x＜4
，作出图象，利用f（1）=3，即可得出结论．
解答： 解：f（x）=x|x-4|=
(x-2)2-4，x≥4
-(x-2)2+4，x＜4
，图象如图所示，
f（1）=3，则x（4-x）=3，可得x=1或3，
x（x-4）=3（x＞4），可得x=2+
7
，
∴不等式f（x）≥f（1）的解集为[1，3]∪[2+
7
，+∞)．
故答案为：[1，3]∪[2+
7
，+∞)．
点评：本题考查绝对值不等式，考查数形结合的数学思想，考查学生分析解决问题的能力，正确作出图象是关键．
练习册系列答案
相关题目
设f（x）=
-x2+2x+1(x≥0)
e-x(x＜0)
关于x的方程f（x）=m（m∈R）恰有三个互不相等的实数根x1，x2，x3，则x1x2x3的取值范围是
 
．
已知数列{an}满足a1=1，2n-1an=an-1（n∈N*，n≥2）．
（1）求数列{an}的通项公式；
（2）此数列从第几项开始，这一项及以后各项均小于
1
1000
？
已知双曲线C1：
x2
a2
-
y2
b2
=1（a＞0，b＞0）与C2：
y2
b2
-
x2
a2
=1（a＞0，b＞0），给出下列四个结论：
①C1与C2的焦距相等；
②C1与C2的离心率相等；
③C1与C2的渐近线相同；
④C1的焦点到其渐近线的距离与C2的焦点到其渐近线的距离相等．
其中一定正确的结论是
 
（填序号）．
为了了解中学生的身体发育情况，对某中学17岁的60名女生的身高进行了测量，结果如下：154 159 166 169 159 156 166 162 158 167 156 166 160 164 160 157 151 157 161 162 158 153 158 164 158 163 158 153 157 163 162 159 154 165 166 157 151 146 157 158 160 165 158 163 163 162 161 154 165 159 162 159 157 159 149 164 168 159 153 160，根据数据列出样本的频率分布表，绘出频率直方图．
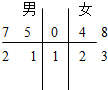某校高三年级共有300人参加数学期中考试，从中随机抽取4名男生和4名女生的试卷，获得某一道题的样本，该题得分的茎叶图如图．
（Ⅰ） 求样本的平均数；
（Ⅱ） 设该题得分大于样本的平均数为合格，根据样本数据估计该校高三年级有多少名同学此题成绩合格；
（Ⅲ）在这4名男生和4名女生中，分别随机抽取一人，求该题女生得分不低于男生得分的概率．
在平面直角坐标系xOy中，直线
x=a-t
y=t
（t为参数）与圆
x=1+cosθ
y=sinθ
（θ为参数）相切，切点在第一象限，则实数a的值为（　　）
A、
2
+1
B、
2
-1
C、1
D、
2
已知函数f（x）=x•ㄧxㄧ-2x．
（Ⅰ）求函数f（x）的零点；
（Ⅱ）画出y=f（x）的图象，并结合图象写出f（x）=m有三个不同实根时，实数m的取值范围；
（Ⅲ）写出函数f（x）的单调区间．
已知数列{an}满足a1=1，且anan+1=2n，则数列{an}的前20项的和为（　　）
A、3×211-3
B、3×211-1
C、3×210-2
D、3×210-5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网