题目内容
1.设命题p:直线mx-y+1=0与圆(x-2)2+y2=4有公共点;设命题q:实数m满足方程$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{2-m}$=1表示双曲线.(1)若“p∧q”为真命题,求实数m的取值范围;
(2)若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
分析 求出p,q成立的等价条件,
(Ⅰ)若“p∧q”为真命题,则p真q真,即可求实数m的取值范围;
(Ⅱ)若“p∧q”为假命题,“p∨q”为真命题,则p、q一真一假,当p真q假时,求出m的取值范围,当p假q真时,求出m的取值范围,然后取并集即可得答案.
解答 解:若命题p:直线mx-y+1=0与圆(x-2)2+y2=4有公共点是真命题,
则圆心(2,0)到直线mx-y+1=0的距离不大于半径,
即$\frac{|2m+1|}{\sqrt{{m}^{2}+1}}≤2$,
解得:$m≤\frac{3}{4}$.
∴命题p真时,$m≤\frac{3}{4}$.
命题p假时,$m>\frac{3}{4}$.
命题q:实数m满足方程$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{2-m}$=1表示双曲线是真命题,
则(m-1)(2-m)<0,解得m<1或m>2.
命题q假时,1≤m≤2.
(1)若“p∧q”为真命题,则p真q真,∴$\left\{\begin{array}{l}{m≤\frac{3}{4}}\\{m<1或m>2}\end{array}\right.$,解得m≤$\frac{3}{4}$.
∴实数m的取值范围为:(-∞,$\frac{3}{4}$];
(2)若“p∧q”为假命题,“p∨q”为真命题,则p、q一真一假,
当p真q假时,则$\left\{\begin{array}{l}{m≤\frac{3}{4}}\\{1≤m≤2}\end{array}\right.$,不存在满足条件的m值.
当p假q真时,则$\left\{\begin{array}{l}{m>\frac{3}{4}}\\{m<1或m>2}\end{array}\right.$,解得$\frac{3}{4}<m<1$.
综上,实数m的取值范围为:($\frac{3}{4}$,1).
点评 本题考查了命题的真假判断与应用,考查了直线与圆的位置关系,双曲线的定义,复合命题等知识点,是中档题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 阅读如图所示的程序框图,程序结束时,输出S的值为( )
阅读如图所示的程序框图,程序结束时,输出S的值为( )| A. | 6 | B. | 21 | C. | 58 | D. | 141 |
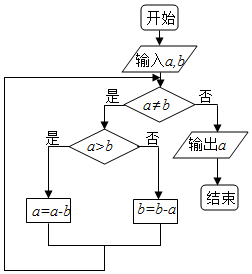 《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )
《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )| A. | 288 | B. | 294 | C. | 378 | D. | 399 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | 1 |
| A. | $\overline{x}$,s2 | B. | $\overline{x}$+200,s2 | C. | $\overline{x}$,2002s2 | D. | $\overline{x}$+200,s2+2002 |
| A. | 90° | B. | 120° | C. | 150° | D. | 180° |