题目内容
在△ABC中,若
=3,b2-a2=
ac,则cosB的值为( )
| sinC |
| sinA |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:余弦定理
专题:三角函数的求值
分析:已知第一个等式利用正弦定理化简,得到c=3a,代入第二个等式变形出b,利用余弦定理表示出cosB,将表示出的b与c代入即可求出值.
解答:
解:将
=3利用正弦定理化简得:
=3,即c=3a,
把c=3a代入b2-a2=
ac,得:b2-a2=
ac=
a2,即b2=
a2,
则cosB=
=
=
.
故选:D.
| sinC |
| sinA |
| c |
| a |
把c=3a代入b2-a2=
| 5 |
| 2 |
| 5 |
| 2 |
| 15 |
| 2 |
| 17 |
| 2 |
则cosB=
| a2+c2-b2 |
| 2ac |
a2+9a2-
| ||
| 6a2 |
| 1 |
| 4 |
故选:D.
点评:此题考查了正弦、余弦定理,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
某程序框图如图所示,若程序运行后,输出S的结果是( )


| A、143 | B、120 |
| C、99 | D、80 |
如图所示的算法框图中,语句“输出i”被执行的次数为( )


| A、32 | B、33 | C、34 | D、35 |
运行如图所示的程序框图,则输出的结果是( )


A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
在空间中,设α,β表示平面,m,n表示直线.则下列命题正确的是( )
| A、若m∥n,n⊥α,则m⊥α |
| B、若α⊥β,m?α,则m⊥β |
| C、若m上有无数个点不在α内,则m∥α |
| D、若m∥α,那么m与α内的任何直线平行 |
如图所示的程序框图输出的结果是S=720,则判断框内应填的条件是( )

| A、i≤7 | B、i>7 |
| C、i≤9 | D、i>9 |

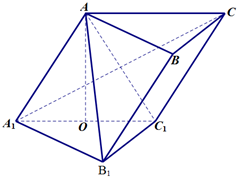 如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.