题目内容
3.某电脑公司2016年的各项经营总收入中电脑配件的收入为40万元,占全年经营总收入的40%,该公司预计2018年经营总收入要达到169万元,且计划从2016年到2018年每年经营总收入的年增长率相同,则2017年预计经营总收入为130万元.分析 增长率问题的一般形式为a(1+x)2=b,a为起始时间的有关数量,b为终止时间的有关数量.本题中a就是2016年的经营收入,b就是2018年的经营收入,从而可求出增长率的值,进而可求2017年预计经营总收入.
解答 解:2016年的经营总收入为400÷40%=1000(万元).
设年增长率为x(x>0),依题意得,1000(1+x)2=169,
解得:x1=0.3,x2=-2.3,
∵x>0
∴x2=-2.3不合题意,
∴只取x1=0.3.
1000(1+x)=1000×1.3=130(万元).
即2017年预计经营总收入为130万元.
故答案为:130.
点评 本题以实际问题为载体,考查增长率问题.解决此类两次变化问题,可利用公式a(1+x)2=b,其中a是变化前的原始量,b是两次变化后的量,x表示平均每次的增长率.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
13.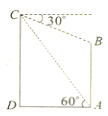 如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )
如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )
 如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )
如图,在热气球C正前方有一高为m的建筑物AB,在建筑物底部A测得C的仰角为60°,同时在C处测得建筑物顶部B的仰角为30°,则此时热气球的高度CD为( )| A. | $\sqrt{2}m$ | B. | $\sqrt{3}m$ | C. | $\frac{{3\sqrt{3}}}{2}m$ | D. | $\frac{3}{2}m$ |
14.已知集合A={-1,0,1,2,3},B={x|(x+1)(x-2)<0,x∈Z},则A∩B=( )
| A. | {1} | B. | {0,1} | C. | {-1,0,1,2} | D. | {-1,0,1,2,3} |
11.已知幂函数f(x)=λ•xα的图象过点$P(\frac{1}{2},\frac{{\sqrt{2}}}{2})$,则λ+α=( )
| A. | 2 | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
18.要得到函数$y=3sin(2x+\frac{π}{3})$图象,只需要将函数$y=3cos(2x-\frac{π}{3})$的图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
8.已知全集U={1,2,3,4,5,6,7,8},A={2,3,5,6},B={1,3,4,6,7},M={x|x∈A,且x∉B},则M=( )
| A. | {2,5} | B. | {3,6} | C. | {2,5,6} | D. | {2,3,5,6,8} |
13.已知命题p:“?x∈R,x2-x+2≥0”,则¬p是( )
| A. | ?x∉R,x2-x+2>0 | B. | ?x0∈R,x02-x0+2≤0 | ||
| C. | ?x0∈R,$x_0^2-{x_0}+2<0$ | D. | ?x0∉R,$x_0^2-{x_0}+2≤0$ |