题目内容
1.已知函数f(x)是定义在R上的奇函数,f(x+2)=f(x),当x∈[0,1]时,f(x)=1-2|x-$\frac{1}{2}$|,求方程f[f(x)]=$\frac{5}{4(x-1)}$在区间[-1,3]上的不等实根之和.分析 由题意可得函数f(x)的图象关于原点对称,为周期为2的函数,求得一个周期的解析式和图象,由图象平移可得[-1,3]的图象,再由y=$\frac{5}{4(x-1)}$的图象关于(1,0)对称,即可得到所求根的和.
解答 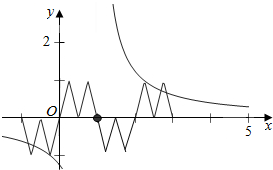 解:函数f(x)是定义在R上的奇函数,f(x+2)=f(x),
解:函数f(x)是定义在R上的奇函数,f(x+2)=f(x),
即有函数f(x)关于原点对称,周期为2,
当x∈(0,1]时,f(x)=1-2|x-$\frac{1}{2}$|,
即有当x∈[-1,0)时,f(x)=-1+2|x+$\frac{1}{2}$|,
由图象的平移可得在区间[-1,3]内的函数f(x)的图象,
进而得到y=f(f(x))的图象,再由y=$\frac{5}{4(x-1)}$的图象
关于(1,0)对称,可得它们有6个交点,都关于(1,0)对称,
则它们的和为2×3=6.
故答案为:6.
点评 本题考查函数和方程的关系,考查函数的性质和运用,主要考查奇偶性和周期性、对称性的运用,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11.由幂函数y=$\sqrt{x}$和幂函数y=x3图象围成的封闭图形的面积为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
16.若不等式x2-2mx+m2-1<0成立的必要不充分条件是$\frac{1}{3}$<x<$\frac{7}{2}$,则实数m的取值范围是( )
| A. | (-∞,$\frac{4}{3}$]∪[$\frac{5}{2}$,+∞) | B. | (-∞,$\frac{4}{3}$]∪($\frac{5}{2}$,+∞) | C. | [$\frac{4}{3}$,$\frac{5}{2}$] | D. | [$\frac{4}{3}$,$\frac{5}{2}$) |
6.已知p:$\frac{1}{x+2}$<0,q:lg(x+2)有意义,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |