题目内容
17.在平面直角坐标系xOy中,P是椭圆$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1上的一个动点,点A(1,1),B(0,-1),则|PA|+|PB|的最大值为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 根据椭圆的方程,算出它的焦点坐标为B(0,-1)和B'(0,1).因此连接PB'、AB',根据椭圆的定义得|PA|+|PB|=|PA|+(2a-|PB'|)=4+(|PA|-|PB'|).再由三角形两边之差小于第三边,得到当且仅当点P在AB'延长线上时,|PA|+|PB|=4+|AB'|=5达到最大值,从而得到本题答案.
解答 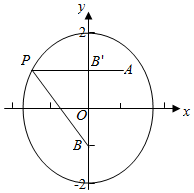 解:∵椭圆$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1,
解:∵椭圆$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1,
∴焦点坐标为B(0,-1)和B'(0,1),
连接PB'、AB',根据椭圆的定义,
得|PB|+|PB'|=2a=4,可得|PB|=4-|PB'|,
因此|PA|+|PB|=|PA|+(4-|PB'|)=4+(|PA|-|PB'|)
∵|PA|-|PB'|≤|AB'|
∴|PA|+|PB|≤2a+|AB'|=4+1=5.
当且仅当点P在AB'延长线上时,等号成立.
综上所述,可得|PA|+|PB|的最大值为5.
故选:A.
点评 本题给出椭圆内部一点A,求椭圆上动点P与A点和一个焦点B的距离和的最大值,着重考查了椭圆的定义、标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
7.已知$p:ab>0;q:\frac{b}{a}+\frac{a}{b}≥2$,则( )
| A. | p是q的充分而不必要条件 | B. | p是q的必要而不充分条件 | ||
| C. | p是q的充要条件 | D. | p是q的既不充分也不必要条件 |
8.若log9(3a+4b)=log3$\sqrt{ab}$,则a+b的最小值是( )
| A. | $6+2\sqrt{3}$ | B. | $7+2\sqrt{3}$ | C. | $6+4\sqrt{3}$ | D. | $7+4\sqrt{3}$ |
2.已知函数$f(x)=lnx-x+\frac{1}{x}$,若a=f(3),b=f(π),c=f(5),则( )
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | a<c<b |
7.已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx,设a=f($\frac{6}{5}$),b=f($\frac{3}{2}$),c=f($\frac{1}{2}$),则( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
 有一块以点O为圆心,半径为2百米的圆形草坪,草坪内距离O点$\sqrt{2}$百米的D点有一用于灌溉的水笼头,现准备过点D修一条笔直小路交草坪圆周于A,B两点,为了方便居民散步,同时修建小路OA,OB,其中小路的宽度忽略不计.
有一块以点O为圆心,半径为2百米的圆形草坪,草坪内距离O点$\sqrt{2}$百米的D点有一用于灌溉的水笼头,现准备过点D修一条笔直小路交草坪圆周于A,B两点,为了方便居民散步,同时修建小路OA,OB,其中小路的宽度忽略不计. 如图,在四棱锥P-ABCD中,侧棱PA⊥平面ABCD,E为AD的中点,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1;
如图,在四棱锥P-ABCD中,侧棱PA⊥平面ABCD,E为AD的中点,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1;