题目内容
9.O为坐标原点,已知向量$\overrightarrow{OA}=({1,5}),\overrightarrow{OB}=({4,-1}),\overrightarrow{OC}=({6,8}),x,y$为非负数实数,且0≤x+y≤1,$\overrightarrow{CD}=x\overrightarrow{CA}+y\overrightarrow{CB}$,则$|{\overrightarrow{OD}}|$的最小值为$\frac{7\sqrt{5}}{5}$.分析 如图所示,x,y非负数实数,且0≤x+y≤1,$\overrightarrow{CD}=x\overrightarrow{CA}+y\overrightarrow{CB}$,则点D表示的区域为△ABC及其内部的点.
当OD⊥AB时,$|{\overrightarrow{OD}}|$取得最小值.
解答 解:如图所示,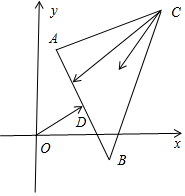 x,y非负数实数,且0≤x+y≤1,$\overrightarrow{CD}=x\overrightarrow{CA}+y\overrightarrow{CB}$,
x,y非负数实数,且0≤x+y≤1,$\overrightarrow{CD}=x\overrightarrow{CA}+y\overrightarrow{CB}$,
则点D表示的区域为△ABC及其内部的点.
当OD⊥AB时,$|{\overrightarrow{OD}}|$取得最小值,
由直线AB的方程为:y+1=$\frac{-1-5}{4-1}$(x-4),
化为:2x+y-7=0.
∴则$|{\overrightarrow{OD}}|$的最小值=$\frac{|0-7|}{\sqrt{5}}$=$\frac{7\sqrt{5}}{5}$.
故答案为:$\frac{7\sqrt{5}}{5}$.
点评 本题考查了向量共线定理、平面向量基本定理、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知随机变量η,ξ具有关系η=3ξ+2,且E(ξ)=1,D(η)=9,则下列式子中正确的是( )
| A. | E(η)=5,D(ξ)=3 | B. | E(η)=3,D(ξ)=27 | C. | E(η)=9,D(ξ)=81 | D. | E(η)=5,D(ξ)=1 |
17.在平面直角坐标系xOy中,P是椭圆$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1上的一个动点,点A(1,1),B(0,-1),则|PA|+|PB|的最大值为( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
18.已知集合M={0,2},无穷数列{an}满足an∈M,且$t=\frac{a_1}{3}+\frac{a_2}{3^2}+\frac{a_3}{3^3}+…+\frac{{{a_{100}}}}{{{3^{100}}}}$,则实数t一定不属于( )
| A. | [0,1) | B. | (0,1] | C. | $[\frac{1}{3},\frac{2}{3})$ | D. | $(\frac{1}{3},\frac{2}{3}]$ |
19.已知z1、z2为复数,且|z1|=2,若z1+z2=2i,则|z1-z2|的最大值是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |