如果直线3ax+y-1=0与直线x+ay+1=0平行．那么a等于$\frac{1}{3}$．题目和参考答案——青夏教育精英家教网—

题目内容

8．如果直线3ax+y-1=0与直线（1-2a）x+ay+1=0平行．那么a等于$\frac{1}{3}$．

分析由平行关系可得a的方程，解方程验证排除重合可得．

解答解：∵直线3ax+y-1=0与直线（1-2a）x+ay+1=0平行，
∴3a•a=1•（1-2a），解得a=-1或a=$\frac{1}{3}$，
经检验当a=-1时，两直线重合，应舍去
故答案为：$\frac{1}{3}$．

点评本题考查直线的一般式方程和平行关系，属基础题．

练习册系列答案

19．设O为坐标原点，A（2，1），若点B（x，y）满足$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}≤1}\\{\frac{1}{2}≤x≤1}\\{0≤y≤1}\end{array}\right.$，则$\overrightarrow{OA}•\overrightarrow{OB}$的最大值是$\sqrt{5}$．

16．i是虚数单位，复数2i=z（-1+i），则z的共轭复数是（　　）

3．已知圆锥的母线长是10，侧面展开图是半圆，则该圆锥的侧面积为（　　）

13．已知顶点是坐标原点，对称轴是x轴的抛物线经过点M（$\frac{1}{2}$，-$\sqrt{2}$）．
（I）求抛物线的标准方程；
（Ⅱ）直线l过点P（1，0），且与抛物线交于不同两点A，B，若|AB|=5，求直线l的方程．

20．

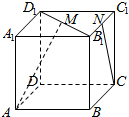正方体ABCD-A₁B₁C₁D₁的棱长为2，点M和N分别是B₁D₁和B₁C₁的中点，则异面直线AM和CN所成角的余弦值为$\frac{\sqrt{30}}{10}$．

17．方程$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{2}$-$\frac{{z}^{2}}{3}$=1表示的曲面是（　　）

18．已知抛物线M的顶点在原点，焦点为（0，$\frac{1}{4}$），半径为1的圆N的圆心N（0，b）在直线l：4x-4y+5=0上．
（1）求抛物线M与圆N的标准方程；
（2）直线1与抛物线M相交于A、B两点，求弦AB的长；
（3）求圆N的圆心到抛物线M的最短距离．

试题分类