题目内容
9.已知函数f(x)=a+$\sqrt{x}$lnx(a∈R).(1)求f(x)的单调区间;
(2)试求f(x)的零点个数,并证明你的结论.
分析 (1)求出函数的导数,解关于导函数的不等式,从而求出函数的单调区间;
(2)求出函数的最小值,通过讨论a的范围,从而求出函数的零点的个数即可.
解答 解:(1)由函数f(x)=a+$\sqrt{x}$lnx(a∈R),得f′(x)=$\frac{1}{2\sqrt{x}}$(lnx+2).
另f′(x)=0,得x=e-2.列表如下:
| x | (0,e-2) | e-2 | (e-2,+∞) |
| f′(x) | - | 0 | + |
| f(x) |  | 极小值 |  |
(2)由(1)可知,fmin(x)=f(e-2)=a-2e-1.
(i)当a>2e-1时,由f(x)≥f(e-2)=a-2e-1>0,得函数f(x)的零点个数为0.
(ii)当a=2e-1时,因f(x)在(e-2,+∞)上是单调增,在(0,e-2)上单调减,
故x∈(0,e-2)∪(e-2,+∞)时,f(x)>f(e-2)=0.
此时,函数f(x)的零点个数为1.
(iii)当a<2e-1时,fmin(x)=a-2e-1<0.
①a≤0时,因为当x∈(0,e-2]时,f(xa+$\sqrt{x}$lnx<x≤0,
所以,函数f(x)在区间(0,e-2]上无零点;
另一方面,因为f(x)在[e-2,+∞)单调递增,且f(e-2)=a-2e-1<0,
由e-2a∈(e-2,+∞),且f(e-2a)=a(1-2e-a)>0,
此时,函数f(x)在(e-2,+∞)上有且只有一个零点.
所以,当a≤0时,函数f(x)零点个数为1.
②0<a<2e-1时,因为f(x)在[e-2,+∞)上单调递增,且f(1)=a>0,f(e-2)=a-2e-1<0,
所以函数f(x)在区间(e-2,+∞)上有且只有一个零点;
另一方面,因为f(x)在(0,e2]上是单调递减,且f(e-2)=a-2e-1<0
又e${\;}^{-\frac{4}{a}}$∈(0,e-2),且f(e${\;}^{-\frac{4}{a}}$)=a-$\frac{4}{a{e}^{\frac{2}{a}}}$>a-$\frac{4}{a(\frac{2}{a})^{2}}$=0,(当x>0时,ex>x2成立)
此时,函数f(x)在(0,e2)上有且只有一个零点.
所以,当0<a<2e-1,函数f(x)的零点个数为2.
综上所述,当a>2e-1时,f(x)的零点个数为0;
当a=2e-1时,或a≤0时,f(x)的零点个数为1;
当0<a<2e-1时,f(x)的零点个数为2.
点评 本题考察了导数的应用,考察函数的单调性问题,函数的零点问题,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.方程$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{2}$-$\frac{{z}^{2}}{3}$=1表示的曲面是( )
| A. | 旋转双曲面 | B. | 旋转椭球面 | C. | 旋转抛物面 | D. | 椭圆抛物面 |
1.从装有3个红球和2个黑球的口袋内任取2个球,那么对立的两个事件是( )
| A. | 至少有1个黑球与都是红球 | B. | 至少有1个黑球与都是黑球 | ||
| C. | 至少有1个黑球与至少有1个红球 | D. | 恰有1个黑球与恰有2个黑球 |
19.设f(1-x)=$\frac{x+1}{2x-1}$,则f(x)=( )
| A. | $\frac{x}{2x-1}$ | B. | $\frac{x-2}{1-2x}$ | C. | $\frac{x+1}{2x-1}$ | D. | $\frac{2-x}{1-2x}$ |
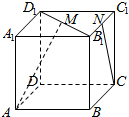 正方体ABCD-A1B1C1D1的棱长为2,点M和N分别是B1D1和B1C1的中点,则异面直线AM和CN所成角的余弦值为$\frac{\sqrt{30}}{10}$.
正方体ABCD-A1B1C1D1的棱长为2,点M和N分别是B1D1和B1C1的中点,则异面直线AM和CN所成角的余弦值为$\frac{\sqrt{30}}{10}$.