题目内容
10.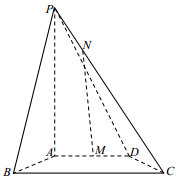 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,BC=2AD=4,AB=CD,∠ABC=60°,N为线段PC上一点,CN=3NP,M为AD的中点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,BC=2AD=4,AB=CD,∠ABC=60°,N为线段PC上一点,CN=3NP,M为AD的中点.(1)证明:MN∥平面PAB;
(2)求点N到平面 PAB的距离.
分析 (1)过N作NE∥BC,交PB于点E,连AE,推导出四边形AMNE是平行四边形,从而MN∥AE,由此能证明MN∥平面PAB.
(2)连接AC,推导出AC⊥AB,PA⊥AC,从而AC⊥平面PAB,由此能求出N点到平面PAB的距离.
解答 证明:(1)过N作NE∥BC,交PB于点E,连AE,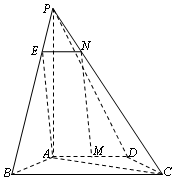
∵CN=3NP,∴EN∥BC且EN=$\frac{1}{4}$BC,
又∵AD∥BC,BC=2AD=4,M为AD的中点,
∴AM∥BC且AM=$\frac{1}{4}$BC,
∴EN∥AM且EN=AM,
∴四边形AMNE是平行四边形,∴MN∥AE,
又∵MN?平面PAB,AE?平面PAB,
∴MN∥平面PAB.…(6分)
解:(2)连接AC,在梯形ABCD中,
由BC=2AD=4,AB=CD,∠ABC=60°,得AB=2,
∴AC=2$\sqrt{3}$,AC⊥AB.
∵PA⊥平面ABCD,∴PA⊥AC.
又∵PA∩AB=A,∴AC⊥平面PAB.
又∵CN=3NP,
∴N点到平面PAB的距离d=$\frac{1}{4}$AC=$\frac{\sqrt{3}}{2}$.…(12分)
点评 本题考查线面平行的证明,考查点到平面的距离的求不地,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
18.已知集合 A={-2,-1,0,2,3},B={y|y=|x|,x∈A},则A∩B=( )
| A. | {0,1,2,3} | B. | {2,3} | C. | {0,1,2} | D. | {0,2,3} |
15.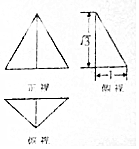 已知三棱锥的三视图如图所示,其中俯视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )
已知三棱锥的三视图如图所示,其中俯视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )
 已知三棱锥的三视图如图所示,其中俯视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )
已知三棱锥的三视图如图所示,其中俯视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
19.已知直线l1:(m-2)x-y+5=0与l2:(m-2)x+(3-m)y+2=0平行,则实数m的值为( )
| A. | 2或4 | B. | 1或4 | C. | 1或2 | D. | 4 |
20.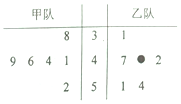 甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )
甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )
 甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )
甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
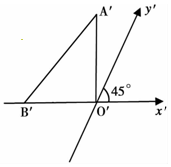 如图所示,△A′O′B′表示水平放置△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′O′=8,则△AOB的边OB上的高为16$\sqrt{2}$.
如图所示,△A′O′B′表示水平放置△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′O′=8,则△AOB的边OB上的高为16$\sqrt{2}$.