题目内容
在平面直角坐标系xOy中,已知圆x2+y2-12x+32=0的圆心为Q,过点P(0,2)且斜率为k的直线与圆Q相交于不同的两点A,B.
(1)求k的取值范围;
(2)求AB中点的轨迹方程;
(3)以OA,OB为邻边作平行四边形OADB,是否存在常数k,使得直线OD与PQ平行?如果存在,求k值;如果不存在,请说明理由.
(1)求k的取值范围;
(2)求AB中点的轨迹方程;
(3)以OA,OB为邻边作平行四边形OADB,是否存在常数k,使得直线OD与PQ平行?如果存在,求k值;如果不存在,请说明理由.
考点:轨迹方程,直线与圆的位置关系
专题:圆锥曲线中的最值与范围问题
分析:(1)先把圆的方程整理成标准方程,进而求得圆心,设出直线方程代入圆方程整理后,根据判别式大于0求得k 的范围.
(2)设A(x1,y1),B(x2,y2),AB中点M(x,y),则x1+x2=2x,y1+y2=2y,把A(x1,y1),B(x2,y2)分别代入圆x2+y2-12x+32=0,利用点差法能求出AB中点的轨迹方程.
(3)A(x1,y1),B(x2,y2),根据(1)中的方程和韦达定理可求得x1+x2的表达式,根据直线方程可求得y1+y2的表达式,进而根据直线OD与PQ平行可推知(x1+x2)=-3(y1+y2),进而求得k,根据(1)k的范围可知,k不符合题意.
(2)设A(x1,y1),B(x2,y2),AB中点M(x,y),则x1+x2=2x,y1+y2=2y,把A(x1,y1),B(x2,y2)分别代入圆x2+y2-12x+32=0,利用点差法能求出AB中点的轨迹方程.
(3)A(x1,y1),B(x2,y2),根据(1)中的方程和韦达定理可求得x1+x2的表达式,根据直线方程可求得y1+y2的表达式,进而根据直线OD与PQ平行可推知(x1+x2)=-3(y1+y2),进而求得k,根据(1)k的范围可知,k不符合题意.
解答:
解:(1)圆的方程可写成(x-6)2+y2=4,
所以圆心为Q(6,0),过P(0,2)
且斜率为k的直线方程为y=kx+2.
代入圆方程得x2+(kx+2)2-12x+32=0,
整理得(1+k2)x2+4(k-3)x+36=0. ①
直线与圆交于两个不同的点A,B等价于:
△=[4(k-3)2]-4×36(1+k2)=42(-8k2-6k)>0,
解得-
<k<0,即k的取值范围为(-
,0).
(2)设A(x1,y1),B(x2,y2),AB中点M(x,y),
则x1+x2=2x,y1+y2=2y,
把A(x1,y1),B(x2,y2)分别代入圆x2+y2-12x+32=0,得:
,
两式相减,得(x1+x2)(x1-x2)+(y1+y2)(y1-y2)-12(x1-x2)=0,
∴(2x-12)(x1-x2)+2y(y1-y2)=0,
∴k=
=
,
又∵直线AB过M(x,y),P(0,2),∴k=
,
∴中点M的轨迹方程为
=
,整理,得:x2+y2-6x-2y=0.
(3)设A(x1,y1),B(x2,y2),则
=
+
=(x1+x2,y1+y2),
由方程①,x1+x2=-
②
又y1+y2=k(x1+x2)+4. ③
而P(0,2),Q(6,0),
=(6,-2).
∵直线OD与PQ平行,∴(x1+x2)=-3(y1+y2),
将②③代入上式,解得k=-
.
∵k的取值范围为(-
,0),∴没有符合题意的常数k.
故存在常数k,使得直线OD与PQ平行.
所以圆心为Q(6,0),过P(0,2)
且斜率为k的直线方程为y=kx+2.
代入圆方程得x2+(kx+2)2-12x+32=0,
整理得(1+k2)x2+4(k-3)x+36=0. ①
直线与圆交于两个不同的点A,B等价于:
△=[4(k-3)2]-4×36(1+k2)=42(-8k2-6k)>0,
解得-
| 3 |
| 4 |
| 3 |
| 4 |
(2)设A(x1,y1),B(x2,y2),AB中点M(x,y),
则x1+x2=2x,y1+y2=2y,
把A(x1,y1),B(x2,y2)分别代入圆x2+y2-12x+32=0,得:
|
两式相减,得(x1+x2)(x1-x2)+(y1+y2)(y1-y2)-12(x1-x2)=0,
∴(2x-12)(x1-x2)+2y(y1-y2)=0,
∴k=
| y1-y2 |
| x1-x2 |
| 6-x |
| y |
又∵直线AB过M(x,y),P(0,2),∴k=
| y-2 |
| x |
∴中点M的轨迹方程为
| 6-x |
| y |
| y-2 |
| x |
(3)设A(x1,y1),B(x2,y2),则
| OD |
| OA |
| OB |
由方程①,x1+x2=-
| 4(k-3) |
| 1+k2 |
又y1+y2=k(x1+x2)+4. ③
而P(0,2),Q(6,0),
| PQ |
∵直线OD与PQ平行,∴(x1+x2)=-3(y1+y2),
将②③代入上式,解得k=-
| 3 |
| 4 |
∵k的取值范围为(-
| 3 |
| 4 |
故存在常数k,使得直线OD与PQ平行.
点评:本题主要考查了直线与圆的方程的综合运用.常需要把直线方程与圆的方程联立,利用韦达定理和判别式求得问题的解,是中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知集合M={x|x-2<0},N={x|x<a},若M⊆N,则实数a的取值范围是( )
| A、[2,+∞) |
| B、(2,+∞) |
| C、(-∞,0) |
| D、(-∞,0] |
已知命题:p:在△ABC中,sinA>sinB的充分不必要条件是A>B;q:?x∈R,x2+2x+2≤0.则下列命题为真命题的是( )
| A、p∧q | B、¬p∧q |
| C、¬p∨q | D、p∨q |
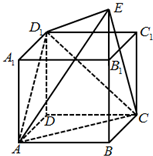 如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,|BB1|=a,E为BB1延长线上的一点且满足|BB1|•|B1E|=1.
如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,|BB1|=a,E为BB1延长线上的一点且满足|BB1|•|B1E|=1.