题目内容
20.设实数x,y满足$\left\{\begin{array}{l}{x-y≥0}\\{x+y-2≤0}\\{y≥-1}\end{array}\right.$(1)作出不等式组表示的平面区域,并计算出不等式组表示平面区域的面积;
(2)求平面区域外接圆方程.
分析 (1)根据二元一次不等式组表示平面区域进行作图即可.
(2)求外接圆的圆心和半径,即可得到结论.
解答 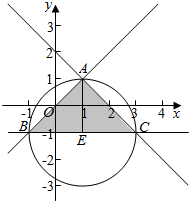 解:(1)作出不等式组对应的平面区域如图:
解:(1)作出不等式组对应的平面区域如图:
在三角形ABC为等腰直角三角形,
其中A(1,1),B(-1,-1),C(3,-1),
则BC=3-(-1)=4,三角形的高h=1-(-1)=2.
则三角形的面积S=$\frac{1}{2}×4×2=4$.
(2)∵三角形ABC为等腰直角三角形,
∴三角形ABC的外接圆的直径是BC,
则BC的中点E(1,-1)为圆心,半径R=$\frac{1}{2}BC$=$\frac{1}{2}×4=2$,
则平面区域外接圆方程为(x-1)2+(y+1)2=4
点评 本题主要考查线性规划的应用以及三角形的外接圆方程的计算,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
11.已知a,b∈R,下列结论成立的是( )
| A. | 若a<b,则ac<bc | B. | 若a<b,c<d,则ac<bd | ||
| C. | 若a<b<0,则$\frac{1}{a}$>$\frac{1}{b}$ | D. | 若a<b,则an<bn(n∈N*,n≥2) |