题目内容
11.某市根据地理位置划分成了南北两区,为调查该市的一种经济作物A(下简称A作物)的生长状况,用简单随机抽样方法从该市调查了500处A作物种植点,其生长状况如表:| 生长指数 | 2 | 1 | 0 | -1 | ||
| 地域 | 南区 | 空气质量好 | 45 | 54 | 26 | 35 |
| 空气质量差 | 7 | 16 | 12 | 5 | ||
| 北区 | 空气质量好 | 70 | 105 | 20 | 25 | |
| 空气质量差 | 19 | 38 | 18 | 5 | ||
(Ⅰ)估计该市空气质量差的A作物种植点中,不绝收的种植点所占的比例;
(Ⅱ)能否有99%的把握认为“该市A作物的种植点是否绝收与所在地域有关”?
(Ⅲ)根据(Ⅱ)的结论,能否提供更好的调查方法来估计该市A作物的种植点中,绝收种植点的比例?并说明理由.
附:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
分析 (I)根据表格数据计算;
(II)采用独立检验方法列联表计算K2,与6.635比较大小得出结论;
(III)根据绝收比例可以看出采用分层抽样比较合理.
解答 解:(1)调查的500处种植点中共有120处空气质量差,其中不绝收的共有110处,
∴空气质量差的A作物种植点中,不绝收的种植点所占的比例$\frac{110}{120}=\frac{11}{12}$.
(2)列联表如下:
| 收 | 绝收 | 合计 | |
| 南区 | 160 | 40 | 200 |
| 北区 | 270 | 30 | 300 |
| 合计 | 430 | 70 | 500 |
∵9.967>6.635,
∴有99%的把握认为“该市A作物的种植点是否绝收与所在地域有关“.
(3)由(2)的结论可知该市A作物的种植点是否绝收与所在地域有关,
因此在调查时,先确定该市南北种植比例,再把种植区分南北两层采用分层抽样比采用简单随机抽样方法好.
点评 本题考查了独立性检验的体积思想,属于基础题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
6.已知|$\overrightarrow a$|=|$\overrightarrow b$|=1,|$\overrightarrow a$-$\overrightarrow b$|=$\sqrt{2}$,则|$\overrightarrow a$+$\overrightarrow b$|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
16.已知集合B={1},A∪B={1,2},则A=( )
| A. | ∅ | B. | {2} | C. | {1,2} | D. | {2}或{1,2} |
3.在某学校进行的一次语文与历史成绩中,随机抽取了25位考生的成绩进行分析,25位考生的语文成绩已经统计在茎叶图中,历史成绩如下:
85 52 64 49 55 71 90 66 46 66 39 61 56
78 67 77 58 73 42 80 72 67 70 51 65
(Ⅰ)请根据数据在茎叶图中完成历史成绩统计;
(Ⅱ)请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图;
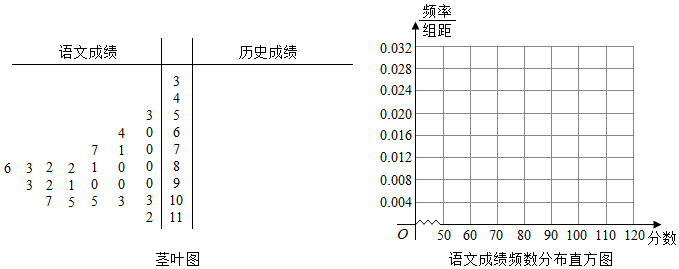
语文成绩的频数分布表:
(Ⅲ)设上述样本中第i位考生的语文、历史成绩分别为xi,yi(i=1,2,…,25).通过对样本数据进行初步处理发现:语文、历史成绩具有线性相关关系,得到:
$\overline{x}$=$\frac{1}{25}$$\sum_{i=1}^{25}$xi=86,$\overline{y}$=$\frac{1}{25}$$\sum_{i=1}^{25}$yi=64,$\sum_{i=1}^{25}$(xi-$\overline{x}$)(yi-$\overline{y}$)=4698,$\sum_{i=1}^{25}$(xi-$\overline{x}$)2=5524,$\frac{4698}{5524}$≈0.85.
①求y关于x的线性回归方程;
②并据此预测,当某考生的语文成绩为100分时,该生历史成绩.(精确到0.1分)
附:回归直线方程的斜率和截距的最小二乘法估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}•{y}_{i}-\overline{n}x•\overline{y}}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
85 52 64 49 55 71 90 66 46 66 39 61 56
78 67 77 58 73 42 80 72 67 70 51 65
(Ⅰ)请根据数据在茎叶图中完成历史成绩统计;
(Ⅱ)请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图;

语文成绩的频数分布表:
| 语文成绩分组 | [50,60) | [60,70) | [70,80) | [90,100) | [100,110) | [110,120] |
| 频数 |
$\overline{x}$=$\frac{1}{25}$$\sum_{i=1}^{25}$xi=86,$\overline{y}$=$\frac{1}{25}$$\sum_{i=1}^{25}$yi=64,$\sum_{i=1}^{25}$(xi-$\overline{x}$)(yi-$\overline{y}$)=4698,$\sum_{i=1}^{25}$(xi-$\overline{x}$)2=5524,$\frac{4698}{5524}$≈0.85.
①求y关于x的线性回归方程;
②并据此预测,当某考生的语文成绩为100分时,该生历史成绩.(精确到0.1分)
附:回归直线方程的斜率和截距的最小二乘法估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}•{y}_{i}-\overline{n}x•\overline{y}}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
20.已知直线l的方程为ax+2y-3=0,且a∈[-5,4],则直线l的斜率不小于1的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{7}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
1. 如图是底面半径为1,高为2的圆柱被削掉一部分后剩余的几何体的三视图(注:正视图也称主视图,侧视图也称左视图),则被削掉的那部分的体积为( )
如图是底面半径为1,高为2的圆柱被削掉一部分后剩余的几何体的三视图(注:正视图也称主视图,侧视图也称左视图),则被削掉的那部分的体积为( )
 如图是底面半径为1,高为2的圆柱被削掉一部分后剩余的几何体的三视图(注:正视图也称主视图,侧视图也称左视图),则被削掉的那部分的体积为( )
如图是底面半径为1,高为2的圆柱被削掉一部分后剩余的几何体的三视图(注:正视图也称主视图,侧视图也称左视图),则被削掉的那部分的体积为( )| A. | $\frac{π+2}{3}$ | B. | $\frac{5π-2}{3}$ | C. | $\frac{5π}{3}$-2 | D. | 2$π-\frac{2}{3}$ |
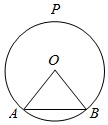 如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧$\widehat{AB}$的中点,设C,D(C在D右侧)为优弧$\widehat{AB}$(不含端点)上的两个不同的动点,且CD∥AB,记∠POD=α,四边形ABCD的面积为S.
如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧$\widehat{AB}$的中点,设C,D(C在D右侧)为优弧$\widehat{AB}$(不含端点)上的两个不同的动点,且CD∥AB,记∠POD=α,四边形ABCD的面积为S.