题目内容
 已知函数y=f(x)的图象如所示,设其定义域为A,值域为C;则对于下列表述:
已知函数y=f(x)的图象如所示,设其定义域为A,值域为C;则对于下列表述:①A=[-5,6);
②A=[-5,0]∪[2,6);
③C=[0,+∞);
④C=[2,5];
⑤方程f(x)=1的解只有一个;
⑥对于值域C中的每一个y,在A中都有唯一的x与之对应;
正确的有
考点:函数的图象
专题:函数的性质及应用
分析:认真观察函数的图象,结合图象能够得到函数y=f(x)的定义域和值域,然后进行判断.
解答:
解:结合图象形状可知,{x|-5≤x≤0}∪{x|2≤x<6}=[-5,0]∪[2,6),
{y|2≤y≤5}∪{y|y≥0}=[0,+∞).
∴函数y=f(x)的定义域是[-5,0]∪[2,6),值域是[0,+∞).
故②③正确,
由图象可知⑤方程f(x)=1的解只有一个是正确的.在值域[2,5]每一个y,在A中都有两个x与之对应,故⑥不正确.
故答案为:②③⑤
{y|2≤y≤5}∪{y|y≥0}=[0,+∞).
∴函数y=f(x)的定义域是[-5,0]∪[2,6),值域是[0,+∞).
故②③正确,
由图象可知⑤方程f(x)=1的解只有一个是正确的.在值域[2,5]每一个y,在A中都有两个x与之对应,故⑥不正确.
故答案为:②③⑤
点评:本题主要考查了识图能力,认真观察图象,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=xln|x|(x≠0)的大致图象是( )
A、 |
B、 |
C、 |
D、 |
阅读程序框图,如果输出的函数值在区间[1,3]上,则输入的实数x的取值范围是( )

| A、{x∈R|0≤x≤log23} |
| B、{x∈R|-2≤x≤2} |
| C、{x∈R|0≤x≤log23,或x=2} |
| D、{x∈R|-2≤x≤log23,或x=2} |
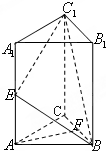 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=4,E、F分别为AA1、BC的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=4,E、F分别为AA1、BC的中点.