题目内容
【题目】已知O是坐标原点,抛物线![]() 的焦点为F,过F且斜率为1的直线交抛物线C于A,B两点,Q为抛物线C的准线上一点,且
的焦点为F,过F且斜率为1的直线交抛物线C于A,B两点,Q为抛物线C的准线上一点,且![]() .
.
(1)求Q点的坐标;
(2)设与直线垂直的直线与抛物线C交于M,N两点,过M,N分别作抛物线C的切线![]() ,
,![]() 设直线
设直线![]() 与
与![]() 交于点P,若
交于点P,若![]() ,求
,求![]() 外接圆的标准方程.
外接圆的标准方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设![]() .根据
.根据![]() .,即
.,即![]() .联立直线和抛物线方程用韦达定理设而不求根据
.联立直线和抛物线方程用韦达定理设而不求根据![]() 代入点的坐标即可求得Q点的坐标;(2)设直线
代入点的坐标即可求得Q点的坐标;(2)设直线![]() 与抛物线联立,根据
与抛物线联立,根据![]() ,即
,即![]() 求出M,N两点横坐标之和和之积。MN为
求出M,N两点横坐标之和和之积。MN为![]() 外接圆的直径,求出MN的中点坐标和MN的长的一半即为半径,从而求得
外接圆的直径,求出MN的中点坐标和MN的长的一半即为半径,从而求得![]() 外接圆的标准方程。
外接圆的标准方程。
(1)由已知得直线的方程为:![]() ,设
,设![]() .
.
由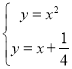 得
得![]() ,
,![]() .∴
.∴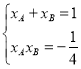 .
.
由![]() 得
得![]() .
.
∴![]() ,解得
,解得![]() .∴Q点的坐标为
.∴Q点的坐标为![]() .
.
(2)设![]() ,
,![]() ,直线
,直线![]() ,
,
由已知得![]() ,
,![]() ,
,
解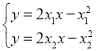 得
得![]() .由题意得
.由题意得![]() ,即
,即![]() .
.
∴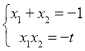 ,
,![]() .
.
∵![]() ,∴
,∴![]() ,解得
,解得![]() .∴
.∴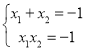 ,
,
∴![]() ,∴
,∴![]() .∴MN为
.∴MN为![]() 外接圆的直径.
外接圆的直径.
又∵![]() ,
,
![]() ,
,
∴![]() 外接圆的圆心为
外接圆的圆心为![]() ,半径为
,半径为![]() .
.
∴![]() 外接圆的标准方程为
外接圆的标准方程为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目