题目内容
【题目】设函数
，曲线
在点
处的切线方程为
.
（1）求
的解析式；
（2）证明：曲线
上任一点处的切线与直线
和直线
所围成的三角形面积为定值，并求此定值.
【答案】(1) 
；(2)证明见解析.
【解析】解：(1)方程7x－4y－12＝0可化为y＝
x－3，
当x＝2时，y＝
．
又f′(x)＝a＋
，
于是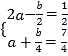
，解得
故f(x)＝x－
．
(2)证明：设P(x0，y0)为曲线上任一点，由f′(x)＝1＋
知，曲线在点P(x0，y0)处的切线方程为y－y0＝(1＋
)·(x－x0)，即y－(x0－
)＝(1＋
)(x－x0)．
令x＝0得，y＝－
，从而得切线与直线x＝0，交点坐标为(0，－ 
)．
令y＝x，得y＝x＝2x0，从而得切线与直线y＝x的交点坐标为(2x0,2x0)．
所以点P(x0，y0)处的切线与直线x＝0，y＝x所围成的三角形面积为
|－
||2x0|＝6．
曲线y＝f(x)上任一点处的切线与直线x＝0和直线y＝x所围成的三角形面积为定值，此定值为6．
练习册系列答案
相关题目
【题目】有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩，得到如下所示的列联表：
优秀 | 非优秀 | 总计 | |
甲班 | 10 |
| |
乙班 |
| 30 | |
总计 |
|
已知在全部105人中随机抽取1人，成绩优秀的概率为
，则下列说法正确的是( )
A. 列联表中
的值为30，
的值为35
B. 列联表中的值为15，的值为50
C. 根据列联表中的数据，若按
的可靠性要求，能认为“成绩与班级有关系”
D. 根据列联表中的数据，若按的可靠性要求，不能认为“成绩与班级有关系”
