题目内容
17.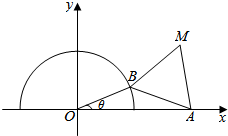 如图,已知半圆O:x2+y2=1(y≥0)及点A(2,0),B为半圆周上任意一点,以AB为一边作等边△ABM.设∠AOB=θ,其中0<θ<π.
如图,已知半圆O:x2+y2=1(y≥0)及点A(2,0),B为半圆周上任意一点,以AB为一边作等边△ABM.设∠AOB=θ,其中0<θ<π.(Ⅰ)将边AB表示为θ的函数;
(Ⅱ)求四边形OAMB面积的最大值.
分析 (Ⅰ)由题意利用余弦定理求得AB的值.
(Ⅱ)四边形OAMB的面积S=S△OAB+S△MAB,利用三角恒等变换化为2sin(θ-$\frac{π}{3}$)+$\frac{5\sqrt{3}}{4}$.再根据0<θ<π,利用正弦函数的值域求得四边形OAMB的面积最大值.
解答 (Ⅰ)解:在△AOB中,由余弦定理得:AB2=OA2+OB2-2OA•OB•cosθ=5-4cosθ,
∴AB=$\sqrt{5-4cosθ}$.
(Ⅱ)解:四边形OAMB的面积 S△OAB+S△MAB=$\frac{1}{2}$•OA•OB•sinθ+$\frac{1}{2}$•AB2•sin$\frac{π}{3}$
=$\frac{1}{2}$•2•sinθ+$\frac{\sqrt{3}}{4}$(5-4cosθ)=sinθ-$\sqrt{3}$cosθ+$\frac{5\sqrt{3}}{4}$=2sin(θ-$\frac{π}{3}$)+$\frac{5\sqrt{3}}{4}$.
又 0<θ<π,则当θ=$\frac{5π}{6}$时,四边形OAMB的面积最大值 2+$\frac{5\sqrt{3}}{4}$.
点评 本题主要考查余弦定理、三角恒等变换、正弦函数的值域,属于中档题.

练习册系列答案
相关题目
12.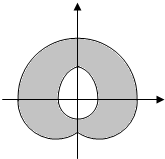 如图是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}中的点在平面上运动时留下的阴影,中间形如“水滴”部分的平面面积为( )
如图是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}中的点在平面上运动时留下的阴影,中间形如“水滴”部分的平面面积为( )
 如图是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}中的点在平面上运动时留下的阴影,中间形如“水滴”部分的平面面积为( )
如图是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}中的点在平面上运动时留下的阴影,中间形如“水滴”部分的平面面积为( )| A. | $\frac{11}{6}π-\sqrt{3}$ | B. | $\frac{7}{3}π-\sqrt{3}$ | C. | $π+\sqrt{3}$ | D. | π+2 |
7.已知x>0,y>0,ln3x+ln9y=ln3,则$\frac{2}{x}+\frac{1}{y}$的最小值是( )
| A. | 6 | B. | $6+\sqrt{2}$ | C. | 8 | D. | $4+2\sqrt{2}$ |