题目内容
16.若直线a∥平面α,直线b在平面α内,则直线a与b的位置关系为( )| A. | 一定平行 | B. | 一定异面 | ||
| C. | 一定相交 | D. | 可能平行、可能异面 |
分析 以正方体AC1为载体,得到直线a∥平面α,直线b在平面α内,则直线a与b的位置关系可能平行、可能异面.
解答  解:如图,在正方体AC1中
解:如图,在正方体AC1中
直线A1B1∥平面ABCD,AB?平面ABCD,BC?平面ABCD,
A1B1∥AB,A1B1与BC异面.
∴直线a∥平面α,直线b在平面α内,则直线a与b的位置关系可能平行、可能异面.
故选:D.
点评 本题考查直线与直线的位置关系的判断,是基础题,解题时要认真审题,注意空间中两直线的位置关系的合理运用.

练习册系列答案
相关题目
6.设$\overrightarrow{a}$,$\overrightarrow{b}$均为非零向量,则“$\overrightarrow{a}$∥$\overrightarrow{b}$”是“$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同”的( )
| A. | 充要条件 | B. | 充分但不必要条件 | ||
| C. | 必要但不充分条件 | D. | 既不充分也不必要条件 |
4.若函数y=f(x)的导函数为y=f′(x),且f′(x)=sin2x-$\sqrt{3}$cos2x,则下列说法正确的是( )
| A. | y=f(x)的周期为$\frac{π}{2}$ | B. | y=f(x)在[0,$\frac{π}{6}$]上是减函数 | ||
| C. | y=f(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=f(x)是偶函数 |
1.已知x,y满足不等式$\left\{\begin{array}{l}x-4y≤-3\\ 3x+5y≤25\\ x≥1\end{array}\right.$,则函数z=2x+y取得最大值是( )
| A. | 3 | B. | $\frac{13}{2}$ | C. | 12 | D. | 23 |
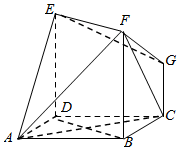 如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.
如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.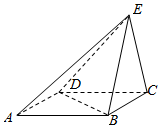 如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.