题目内容
5.设数列{an}的前n项和为Sn,且a1=2,an+1=Sn,n∈N*.(1)写出数列{an}的第5项a5=16;
(2)已知等差数列{bn}中,有b2=a1,b3=a3,设cn=$\frac{b_n}{a_n}$,记数列{cn}的前n项和为Tn,求证:Tn<4(n∈N*).
分析 (1)根据数列的递推公式可以得到数列{Sn}是以2为首相,以2为公比的等比数列,继而求出数列{an}的通项公式,问题得以解决,
(2)先求出数列{bn}的通项公式,再得到数列{cn}的通项公式,根据错位相减法和放缩法即可证明.
解答 解:(1)∵a1=2,an+1=Sn,
∴Sn+1-Sn=Sn,
∴Sn+1=2Sn,
∵S1=a1=2,
∴数列{Sn}是以2为首相,以2为公比的等比数列,
∴Sn=2n,
∴an=2n-1,
∴a5=16
(2)依题意,b2=2,${b_3}={a_3}={2^2}=4$,
所以公差d=b3-b2=2,从而b1=b2-d=2-2=0,
故bn=2(n-1).
∴${c_n}=\left\{{\begin{array}{l}{0,}&{(n=1)}\\{\frac{n-1}{{{2^{n-2}}}},}&{(n≥2)}\end{array}}\right.$,
从而 ${T_n}=0+\frac{1}{2^0}+\frac{2}{2^1}+\frac{3}{2^2}+\frac{4}{2^3}+…+\frac{n-1}{{{2^{n-2}}}}$①
所以$\frac{1}{2}{T_n}=0+\frac{1}{2^1}+\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n-2}{{{2^{n-2}}}}+\frac{n-1}{{{2^{n-1}}}}$②,
①-②得$\frac{1}{2}{T_n}=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{{{2^{n-2}}}}-\frac{n-1}{{{2^{n-1}}}}$$⇒{T_n}=2(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{{{2^{n-2}}}})-\frac{2(n-1)}{{{2^{n-1}}}}$
=$2×\frac{{1×(1-\frac{1}{{{2^{n-1}}}})}}{{1-\frac{1}{2}}}-\frac{2(n-1)}{{{2^{n-1}}}}$=$4×(1-\frac{1}{{{2^{n-1}}}})-\frac{2(n-1)}{{{2^{n-1}}}}$
=$4-\frac{4+2(n-1)}{{{2^{n-1}}}}$
=$4-\frac{4(n+1)}{2^n}$.
∵$\frac{4(n+1)}{2^n}>0$对?n∈N*恒成立,
∴${T_n}\;=4-\frac{4(n+1)}{2^n}<4$对?n∈N*恒成立.
点评 本题考查了数列的通项公式公式的求法和错位相减法求和,以及放缩法证明不等式成立,属于中档题.

(1)投资股市:
| 投资结果 | 获利 | 不赔不赚 | 亏损 |
| 概率 | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| 投资结果 | 获利 | 不赔不赚 | 亏损 |
| 概率 | p | $\frac{1}{3}$ | q |
(Ⅱ)已知“购买基金”亏损的概率比“投资股市”亏损的概率小,求p的取值范围;
(Ⅲ)已知张师傅和李师傅两人都选择了“购买基金”来进行投资,假设三种投资结果出现的可能性相同,求一年后他们两人中至少有一人获利的概率.
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①④ |
| A. | -2或1 | B. | 0或1 | C. | -2或-1 | D. | 0或-2 |
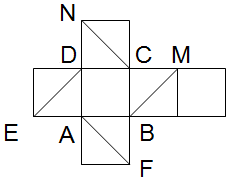 如图是正方体的平面展开图,则下列结论中正确的有(3)(4).
如图是正方体的平面展开图,则下列结论中正确的有(3)(4).