题目内容
7．已知f（2x+1）=x2，则f（5）=4．分析 f（5）=f（2×2+1），由此利用f（2x+1）=x2，能求出结果．
解答 解：∵f（2x+1）=x2，
∴f（5）=f（2×2+1）=22=4．
故答案为：4．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
15．在平面直角坐标系xOy中，已知△ABC的顶点A（0，4），C（0，-4），顶点B在椭圆$\frac{x^2}{9}+\frac{y^2}{25}=1$上，则$\frac{sin（A+C）}{sinA+sinC}$=（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{5}{3}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{4}$ |
2．已知集合I，M，N的关系如图所示，则I，M，N的关系为（ ）
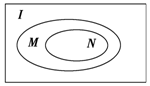
| A． | （∁IM）?（∁IN） | B． | M⊆（∁IN） | C． | （∁IM）⊆（∁IN） | D． | M?（∁IN） |
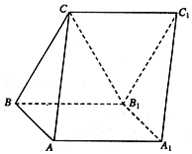如图，三棱柱ABC-A1B1C1的侧面AA1B1B是边长为2的正方形，侧面BB1C1C为菱形，∠CBB1=60°，AB⊥B1C．
17．下列函数既是偶函数又是幂函数的是（ ）
| A． | y=x | B． | $y={x^{\frac{2}{3}}}$ | C． | $y={x^{\frac{1}{2}}}$ | D． | y=|x| |