题目内容
12.已知点P是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1上的动点,F1,F2分别是椭圆C1的左、右焦点,椭圆C2以椭圆C1的长轴为短轴,且与C1有相同的离心率.(1)求椭圆C1的焦点坐标、离心率及PF1的最大值;
(2)求椭圆C2的方程.
分析 (1)求得椭圆C1的a,b,c,可得焦点和离心率,由椭圆上的点与焦点的距离的最大值为a+c,可得;
(2)设椭圆C2的方程为$\frac{{y}^{2}}{{m}^{2}}$+$\frac{{x}^{2}}{{n}^{2}}$=1(m>n>0),由题意可得n=2,再由离心率公式计算即可得到所求方程.
解答 解:(1)椭圆C1:$\frac{{x}^{2}}{4}$+y2=1的a=2,b=1,c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{3}$,
即有F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
PF1的最大值为a+c=2+$\sqrt{3}$;
(2)设椭圆C2的方程为$\frac{{y}^{2}}{{m}^{2}}$+$\frac{{x}^{2}}{{n}^{2}}$=1(m>n>0),
由题意可得n=a=2,e=$\frac{\sqrt{{m}^{2}-{n}^{2}}}{m}$=$\frac{\sqrt{3}}{2}$,
解得m=4,
即有椭圆C2的方程为$\frac{{y}^{2}}{16}$+$\frac{{x}^{2}}{4}$=1.
点评 本题考查椭圆的方程的求法,以及椭圆的性质的运用,注意运用待定系数法,考查运算能力,属于基础题.

练习册系列答案
相关题目
2.已知点E是正方形ABCD的边AD上一动点(端点除外),现将△ABE沿BE所在直线翻折成△A′BE,并连结A′C,A′D.记二面角A′-BE-C的大小为α(0<α<π).则( )
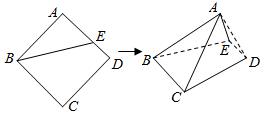

| A. | 存在α,使得BA′⊥面A′DE | B. | 存在α,使得BA′⊥面A′CD | ||
| C. | 存在α,使得EA′⊥面A′CD | D. | 存在α,使得EA′⊥面A′BC |
4.过焦点在x轴上的椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{16}$=1的右焦点F2的直线交椭圆于A,B两点,F1是椭圆的左焦点,若△AF1B的周长为20,则实数m的值为( )
| A. | 5 | B. | 25 | C. | 10 | D. | 100 |
2.已知$sin(-\frac{3}{2}π+θ)=\frac{1}{5}$,则cosθ=( )
| A. | $\frac{1}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $-\frac{2}{5}$ |
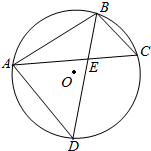 如图,圆O为△ABC的外接圆,D为$\widehat{AC}$的中点,BD交AC于E.
如图,圆O为△ABC的外接圆,D为$\widehat{AC}$的中点,BD交AC于E.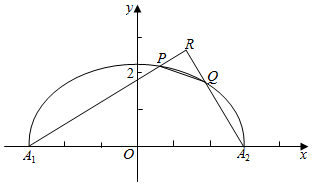 如图,设P是上半椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(y≥0)上任意一点,F为右焦点,PF的最小值是$\sqrt{2}$-1,离心率是$\frac{\sqrt{2}}{2}$,上半椭圆C与x轴交于点A1,A2.
如图,设P是上半椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(y≥0)上任意一点,F为右焦点,PF的最小值是$\sqrt{2}$-1,离心率是$\frac{\sqrt{2}}{2}$,上半椭圆C与x轴交于点A1,A2.