题目内容

1．函数f（x）=ex-2x，则下面判断正确的是（　　）
A．有极小值，无极大值B．有极大值，无极小值
C．既有极小值，也有极大值D．既无极小值，也无极大值

分析 求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而判断函数的极值．

解答 解：f′（x）=ex-2，
令f′（x）＞0，解得：x＞ln2，
令f′（x）＜0，解得：x＜ln2，
∴f（x）在（-∞，ln2）递减，在（ln2，+∞）递增，
∴f（x）有极小值，无极大值，
故选：A．

点评 本题考查了函数的单调性、极值问题，考查导数的应用，是一道基础题．

练习册系列答案
相关题目
10．已知（1+x）（x+$\frac{1}{{x}^{2}}$）n的展开式中没有常数项，则n的值可能是（　　）
A．9B．10C．11D．12
12．已知函数$f（x）=\left\{\begin{array}{l}{2^{x-2}}-1，x≥0\\ x+2，x＜0\end{array}\right，g（x）=\left\{\begin{array}{l}{x^2}-2x，x≥0\\ \frac{1}{x}，x＜0.\end{array}\right.$则函数f[g（x）]的所有零点之和是$\frac{1}{2}$+$\sqrt{3}$．
9．已知函数f（x）=ax2-lnx（a∈R）
（1）若函数y=f（x）图象上点（1，f（1））处的切线方程y=x+b（b∈R），求实数a，b的值；
（2）若y=f（x）在x=2处取得极值，求函数f（x）在区间[$\frac{1}{e}$，e]上的最大值．
16．已知A（3，2，1），B（1，-2，5），则线段AB中点坐标为（2，0，3）．
6．已知函数f（x）=$\frac{ax}{4{x}^{2}+16}$，g（x）=（$\frac{1}{2}$）|x-a|，其中a∈R．
（1）若y=g（x）在[1，$\frac{3}{2}$]上的最大值为$\frac{\sqrt{2}}{2}$，求实数a的值；
（2）设函数p（x）=$\left\{\begin{array}{l}{f（x），x≥2}\\{g（x），x＜2}\end{array}\right.$，若对任意x1∈[2，+∞]，总存在唯一的x2∈（-∞，2），使得p（x1）=p（x2）成立，求实数a的取值范围．
13．已知函数f（x）=2x2-4的图象上一点（1，-2）及邻近一点（1+d，f（1+d）），则$\frac{f（1+d）-f（1）}{d}$等于（　　）
A．4B．4xC．4+2dD．4+2d2
10．已知数列{an}的首项a1=1，前n项和为Sn，且Sn+1=2Sn+n+1（n∈N*）
（1）证明数列{an+1}是等比数列，并求数列{an}的通项公式；
（2）求数列{nan+n}的前n项和Tn．
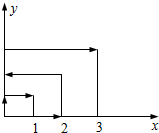11．如图：一个质点在第一象限运动，在第一秒钟它由原点运动到点（0，1），而后接着按图所示在与x轴y轴平行的方向运动，且每秒移动一个单位长度，那么416秒后，这个质点所处的位置的坐标是（20，16）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网