题目内容
12.已知函数$f(x)=\left\{\begin{array}{l}{2^{x-2}}-1,x≥0\\ x+2,x<0\end{array}\right,g(x)=\left\{\begin{array}{l}{x^2}-2x,x≥0\\ \frac{1}{x},x<0.\end{array}\right.$则函数f[g(x)]的所有零点之和是$\frac{1}{2}$+$\sqrt{3}$.分析 先求得f[g(x)]的解析式,x≥0时,由${2}^{{x}^{2}-2x-2}$-1=0,可解得:x=1+$\sqrt{3}$或1-$\sqrt{3}$(小于0,舍去);x<0时,由$\frac{1}{x}$+2=0,可解得:x=-$\frac{1}{2}$,从而可求函数f[g(x)]的所有零点之和.
解答 解:∵$f(x)=\left\{\begin{array}{l}{2^{x-2}}-1,x≥0\\ x+2,x<0\end{array}\right,g(x)=\left\{\begin{array}{l}{x^2}-2x,x≥0\\ \frac{1}{x},x<0.\end{array}\right.$,
∴f[g(x)]=$\left\{\begin{array}{l}{{2}^{{x}^{2}-2x-2}-1,x≥2或x=0}\\{\frac{1}{x}+2,x<0}\end{array}\right.$,且f[g(x)]=x2-2x+2,( 0<x<2)
分情况讨论:①x≥2或x=0时,由2x2-2x-2-1=0,
可解得:x=1+$\sqrt{3}$或1-$\sqrt{3}$(小于0,舍去);
②x<0时,由$\frac{1}{x}$+2=0,可解得:x=-$\frac{1}{2}$,
③当 0<x<2时,由x2-2x+2=0,无解.
∴函数f[g(x)]的所有零点之和是1+$\sqrt{3}$-$\frac{1}{2}$=$\frac{1}{2}$+$\sqrt{3}$,
故答案为:$\frac{1}{2}+\sqrt{3}$.
点评 本题主要考察了函数的零点,函数的性质及应用,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列结论中,错误的为( )
| A. | 对任意的x∈R,都有2x≥x2成立 | |
| B. | 存在实数x0,使得log${\;}_{\frac{1}{2}}$x0>x0 | |
| C. | 存在常数C,当x>C时,都有2x≥x2成立 | |
| D. | 存在实数x0,使得log${\;}_{\frac{1}{2}}$x0>2${\;}^{{x}_{0}}$ |
17.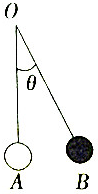 如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )
如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )
 如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )
如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )| A. | $\frac{1}{2}$,$\frac{1}{π}$ | B. | 2,$\frac{1}{π}$ | C. | $\frac{1}{2}$,π | D. | 2,π |
1.函数f(x)=ex-2x,则下面判断正确的是( )
| A. | 有极小值,无极大值 | B. | 有极大值,无极小值 | ||
| C. | 既有极小值,也有极大值 | D. | 既无极小值,也无极大值 |
 如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC,DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}$=$\overrightarrow b$
如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC,DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}$=$\overrightarrow b$