题目内容
10.已知(1+x)(x+$\frac{1}{{x}^{2}}$)n的展开式中没有常数项,则n的值可能是( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 由于(1+x)(x+$\frac{1}{{x}^{2}}$)n的展开式中没有常数项,可知:(x+$\frac{1}{{x}^{2}}$)n的展开式中没有常数项与含$\frac{1}{x}$的项,利用(x+$\frac{1}{{x}^{2}}$)n的展开式中的通项公式即可得出.
解答 解:∵(1+x)(x+$\frac{1}{{x}^{2}}$)n的展开式中没有常数项,∴(x+$\frac{1}{{x}^{2}}$)n的展开式中没有常数项与含$\frac{1}{x}$的项,
(x+$\frac{1}{{x}^{2}}$)n的展开式中的通项公式:Tr+1=${∁}_{n}^{r}$xn-r$(\frac{1}{{x}^{2}})^{r}$=${∁}_{n}^{r}$xn-3r,(r=0,1,2,…,n).
经过验证:只有取n=10时,10-3r≠0,-1.
因此n的值可能是10.
故选:B.
点评 本题考查了二项式定理展开式的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
20.命题“若a<b,则ac2≤bc2”以及它的逆命题,否命题和逆否命题中,真命题的个数是( )
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
1.下列结论中,错误的为( )
| A. | 对任意的x∈R,都有2x≥x2成立 | |
| B. | 存在实数x0,使得log${\;}_{\frac{1}{2}}$x0>x0 | |
| C. | 存在常数C,当x>C时,都有2x≥x2成立 | |
| D. | 存在实数x0,使得log${\;}_{\frac{1}{2}}$x0>2${\;}^{{x}_{0}}$ |
5.设曲线y=xn+1(n∈N*)在(1,1)处的切线与x轴的交点的横坐标为xn,则log2016x1+log2016x2+…+log2016x2015的值为( )
| A. | -log20162015 | B. | -1 | C. | (log20162015)-1 | D. | 1 |
1.函数f(x)=ex-2x,则下面判断正确的是( )
| A. | 有极小值,无极大值 | B. | 有极大值,无极小值 | ||
| C. | 既有极小值,也有极大值 | D. | 既无极小值,也无极大值 |
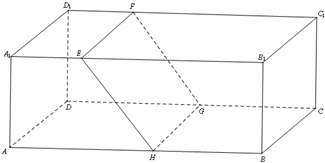 如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.
如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.