题目内容

若△ABC得内角A，B，C所对的边a，b，c满足（a+b）2-c2=2，且C=
π
3
，则ab=（　　）
A、2-
3
B、1
C、
2
3
D、
4
3
考点：余弦定理
专题：计算题,解三角形
分析：将已知的等式展开，利用余弦定理表示出a2+b2-c2求出ab的值．
解答： 解：∵（a+b）2-c2=2，
即a2+b2-c2+2ab=2，
由余弦定理得2abcosC+2ab=2，
∵C=60°，则cosC=
1
2

∴ab=
2
3
，
故选：C．
点评：本题主要考查了三角形中余弦定理的应用，属于基础题．
练习册系列答案
相关题目
已知数列{an}的前n项和Sn满足S1＞1，且6Sn=（an+1）（an+2），n∈N*．
（1）求an与an+1的关系式；
（2）在满足条件的所有数列{an}中，求a2015最小值；
（3）若数列{an}各项都为正数，设数列{bn}满足an（2bn-1）=3，并记Tn为{bn}的前n项和，问：是否存在常数c使得对任意的正整数n，都有Tn≥c成立？如果存在，请写出c的取值范围；如果不存在，请说明理由．
执行如图所示的程序框图，输出的S值为（　　）
A、7B、8C、16D、24
当a＞l时，函数f （x）=logax和g（x）=（l-a）x的图象的交点在（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
数列{an}：2，5，11，20，m，47…猜想{an}中的m等于（　　）
A、27B、28C、31D、32
一个四棱锥的三视图如图所示，则该四棱锥的侧面中，直角三角形的个数为（　　）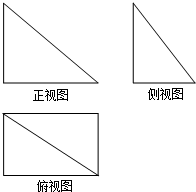
A、1B、2C、3D、4
已知函数f（x）=3x+k（k为常数），A（-2k，2）是函数y=f1（x）图象上的点．
（1）求实数k的值及函数y=f1（x）的解析式：
（2）将y=f1（x）的图象向右平移3个单位，得到函数y=g（x）的图象，若2f1（x+
m
-3}）-g（x）≥1对任意的x＞0恒成立，试求实数m的取值范围．
设a，b，c都是正数，且满足
1
a
+
4
b
=1则使a+b＞c恒成立的c的取值范围是
 
．
已知向量
a
=（cosx，sinx），
b
=（1，1），则函数f（x）=
a
•
b
的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网