Question

偶函数f（x）满足f（x-1）=f（x+1），且在x∈[0，1]时，f（x）=-x+1，则关于x的方程f（x）=（

1

10

）^x，在x∈[1，3]上解的个数是（　　）

• A、1
• B、2
• C、3
• D、4

Answer 1

考点：函数奇偶性的性质

专题：计算题,数形结合,函数的性质及应用

分析：根据已知条件推导函数f（x）的周期，再利用函数与方程思想把问题转化，画出函数的图象，即可求解．

解答： 解：∵f（x-1）=f（x+1）
∴f（x）=f（x+2），
∴原函数的周期T=2．                       
又∵f（x）是偶函数，∴f（-x）=f（x）．
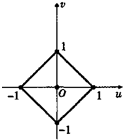
又∵x∈[0，1]时，f（x）=1-x，
则x∈[-1，0]时，f（x）=1+x，
设 y=f（x），y=（

1

10

）^x，
方程f（x）=（

1

10

）^x的根的个数，
即为函数y=f（x）的图象与y=（

1

10

）^x的图象在[1，3]上的交点个数．
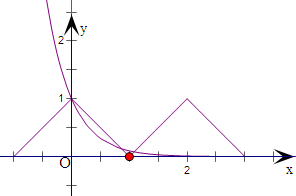
通过图象观察在区间[1，3]上有两个交点．
则解的个数为2．
故选B．

点评：本题考查函数的性质，体现了函数与方程思想，数形结合思想，转化思想，属中档题．