题目内容
10.已知函数f(x)=ln(2+x),g(x)=ln(2-x)(1)求函数y=f(x)-g(x)的定义域;
(2)求使f(x)≥g(x)成立的x的取值范围.
(3)判断函数G(x)=f(x)-g(x)的奇偶性.
分析 (1)根据函数成立的条件即可求函数y=f(x)-g(x)的定义域;
(2)根据对数函数的单调性即可求使f(x)≥g(x)成立的x的取值范围.
(3)根据函数奇偶性的定义即可判断函数G(x)=f(x)-g(x)的奇偶性.
解答 解:(1)y=f(x)-g(x)=ln(2+x)-ln(2-x),
要使函数有意义,则$\left\{\begin{array}{l}{2-x>0}\\{2+x>0}\end{array}\right.$…(3分),
即$\left\{\begin{array}{l}{x<2}\\{x>-2}\end{array}\right.$,即-2<x<2,即函数的定义域为(-2,2).
(2)若f(x)≥g(x),
则ln(2+x)≥ln(2-x)
由(1)且2+x≥2-x得{x|0≤x<2}…(6分)
(3)G(x)定义域为{x|-2<x<2}有关于原点对称…(7分)
G(-x)=f(-x)-g(-x)=$ln(2-x)-ln(2+x)=ln\frac{2-x}{2+x}=ln{(\frac{2+x}{2-x})^{-1}}=-ln\frac{2+x}{2-x}=-G(x)$
所以G(x)为奇函数….(12分)
点评 本题主要考查函数定义域以及函数奇偶性的判断,利用函数奇偶性的定义以及函数单调性的性质是解决本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
19.2007年10月27日全国人大通过了关于修改个所得税的决定,工薪所得减去费用标准从800元提高到1600元,也就是说原来月收入超过800元部分就要纳税,2008年1月1日开始超过1600元才纳税,若税法修改前后超过部分的税率相同,如表:
某人2007年6月交纳个人所得税123元,则按照新税法只要交43元.
| 级数 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过500元 | 5 |
| 2 | 500~2000元 | 10 |
| 3 | 2000~5000元 | 15 |
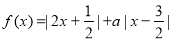 .
.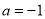 时,解不等式
时,解不等式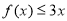 ;
;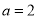 时,若关于
时,若关于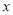 的不等式
的不等式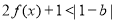 的解集为空集,求实数
的解集为空集,求实数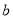 的取值范围.
的取值范围.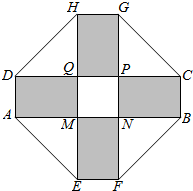 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如△DQH等)上铺草坪,造价为80元/m2.设AD长为xm,DQ长为ym.
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如△DQH等)上铺草坪,造价为80元/m2.设AD长为xm,DQ长为ym.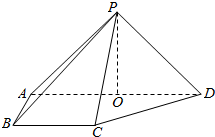 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.