题目内容
求适合下列条件的椭圆的标准方程:已知两焦点F1(-3,0),F2(3,0),且椭圆过(3,
)
| 16 |
| 5 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:设椭圆方程为
+
=1(a>0,b>0),由已知得
,由此能求出椭圆方程.
| x2 |
| a2 |
| y2 |
| b2 |
|
解答:
解:∵两焦点F1(-3,0),F2(3,0),且椭圆过(3,
),
∴设椭圆方程为
+
=1(a>0,b>0),
且
,
解得a=5,b=4,
∴椭圆方程为
+
=1.
| 16 |
| 5 |
∴设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
且
|
解得a=5,b=4,
∴椭圆方程为
| x2 |
| 25 |
| y2 |
| 16 |
点评:本题考查椭圆方程的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
设A(-2,0),B(2,0),条件甲:“△ABC是以C为直角顶点的三角形”;条件乙:“C的坐标是方程x2+y2=4的解”,那么甲是乙的( )
| A、必要非充分条件 |
| B、充要条件 |
| C、充分非必要条件 |
| D、既不充分也非必要条件 |
函数y=
的图象大致为( )
| cos3x |
| 3x-3-x |
A、 |
B、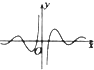 |
C、 |
D、 |