题目内容
已知向量
,
满足|
+
|=4,则
•
的最大值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、1 | B、2 | C、4 | D、8 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由
•
≤|
||
|当且仅当
,
同向共线时取等号,用
=m
(m≥0),利用|
+
|=4,求出
•
的表达式,从而求出
•
的最大值.
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
解答:
解:∵
•
≤|
||
|当且仅当
,
同向共线时取等号,
设
=m
,(m≥0),
由|
+
|=4得(1+m)|
|=4,即|
|=
;
∴
•
=m|
|2=
;
当m=0时,
=0;
当m>0时,
=
≤
=4,当且仅当m=1时取“=”;
∴
•
的最大值是4.
故选:C.
| a |
| b |
| a |
| b |
| a |
| b |
设
| b |
| a |
由|
| a |
| b |
| a |
| a |
| 4 |
| 1+m |
∴
| a |
| b |
| a |
| 16m |
| 1+2m+m2 |
当m=0时,
| 16m |
| 1+2m+m2 |
当m>0时,
| 16m |
| 1+2m+m2 |
| 16 | ||
|
| 16 | ||||
2
|
∴
| a |
| b |
故选:C.
点评:本题考查了平面向量的应用问题,解题时根据平面向量的数量积的定义与性质,结合基本不等式进行解答,是中档题.

练习册系列答案
相关题目
下列选项正确的是( )
| A、映射一定是函数 |
| B、一一映射一定是函数 |
| C、函数一定是一一映射 |
| D、函数一定是映射 |
已知两个数的等差中项是6,等比中项是10,则以这两个数为根的一元二次方程是( )
| A、x2+6x+10=0 |
| B、x2-12x+10=0 |
| C、x2-12x+100=0 |
| D、x2+12x+100=0 |
要得到y=-x2+2x+3的图象,只需将y=-x2的图象经过怎样平移( )
| A、向左平移1个单位,再将所得图象向上平移4个单位 |
| B、向右平移1个单位,再将所得图象向下平移4个单位 |
| C、向左平移1个单位,再将所得图象向下平移4个单位 |
| D、向右平移1个单位,再将所得图象向上平移4个单位 |
已知向量
=(cosθ,sinθ),θ∈[0,π],
=(
,-1),若
∥
,则θ=( )
| a |
| b |
| 3 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
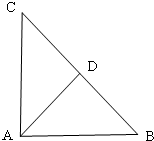 如图△ABC是直角边等于4的等腰直角三角形,D是斜边BC的中点,
如图△ABC是直角边等于4的等腰直角三角形,D是斜边BC的中点,