题目内容
空间四边形ABCD的一组对边BC、AD的长分别为6，4，BC⊥AD，则连接对角线AC，BD中点的线段长为 ．
考点：棱锥的结构特征
专题：计算题,空间位置关系与距离
分析：设AC、BD的中点分别为E、F，取AB的中点G，连接EG、GF，由题设知∠EGF=90°，再由勾股定理能求出连接对角线AC、BD中点的线段长．
解答：
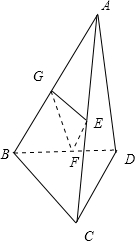解：设AC、BD的中点分别为E、F，取AB的中点G，连接EG、GF，
∵空间四边形ABCD的一组对边BC、AD的长分别为6、4，
∴GE∥BC，GE=3，GF∥AD，GF=2，
∵BC⊥AD，∴∠EGF=90°
∴EF2=GE2+GF2=9+4=13，
∴EF=
．
故答案为：
．
解：设AC、BD的中点分别为E、F，取AB的中点G，连接EG、GF，∵空间四边形ABCD的一组对边BC、AD的长分别为6、4，
∴GE∥BC，GE=3，GF∥AD，GF=2，
∵BC⊥AD，∴∠EGF=90°
∴EF2=GE2+GF2=9+4=13，
∴EF=
| 13 |
故答案为：
| 13 |
点评：本题考查空间中点、线、面间的距离计算，解题时要认真审题，仔细解答，注意等价转化思想的合理运用．
练习册系列答案
相关题目
设t是实数，且
+
是实数，则t的值为（ ）
| t | ||
1-
|
1-
| ||
| 2 |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |