题目内容
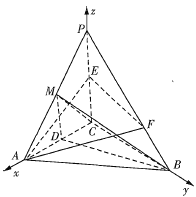
【题目】如图,在三棱锥PABC中,![]() 底面ABC,
底面ABC,![]() ,
,![]() ,
,![]() ,D,E分别是AC,PC的中点,F是PB上一点,且
,D,E分别是AC,PC的中点,F是PB上一点,且![]() ,M为PA的中点,二面角
,M为PA的中点,二面角![]() 的大小为45°.
的大小为45°.

(1)证明:![]() 平面AEF;
平面AEF;
(2)求直线AF与平面BCM所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接PD交AE于点O,因为D,E分别是AC,PC的中点,则点O是![]() 的重心,所以
的重心,所以![]() ,连接OF,又
,连接OF,又![]() ,所以
,所以![]() ,从而可证明结论.
,从而可证明结论.
(2)由题意可证得![]() 即二面角
即二面角![]() 的平面角,即
的平面角,即![]() ,可得
,可得![]() ,则
,则![]() ,得到
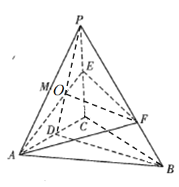
,得到![]() ,又由题意易知,CA,CB,CP两两垂直,故以C为坐标原点,直线CA,CB,CP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系
,又由题意易知,CA,CB,CP两两垂直,故以C为坐标原点,直线CA,CB,CP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系![]() ,用向量法求解线面角.
,用向量法求解线面角.
解:(1)连接PD交AE于点O,因为D,E分别是AC,PC的中点,
所以点O是![]() 的重心,所以
的重心,所以![]() .
.
连接OF,又![]() ,所以
,所以![]() ,则
,则![]() .
.
又![]() 平面AEF,
平面AEF,![]() 平面AEF,所以
平面AEF,所以![]() 平面AEF.
平面AEF.
(2)因为![]() 底面ABC,
底面ABC,![]() 平面ABC,所以
平面ABC,所以![]() .又
.又![]() ,
,![]() ,
,
所以![]() 平面PAC.所以
平面PAC.所以![]() ,又
,又![]() ,所以
,所以![]() 即二面角
即二面角![]() 的平面角,
的平面角,
所以![]() ,连接MD,易得
,连接MD,易得![]() ,则
,则![]() ,所以
,所以![]() .
.
由题意易知,CA,CB,CP两两垂直,故以C为坐标原点,直线CA,CB,CP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,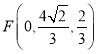 ,
,
所以![]() ,
,![]() ,
,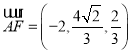 .
.
设平面BCM的法向量为![]() ,则
,则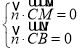 ,得
,得 ,得
,得![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() 为平面BCM的一个法向量.
为平面BCM的一个法向量.
设直线AF与平面BCM所成的角为![]() .
.
则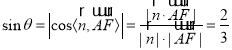
故直线AF与平面BCM所成角的正弦值为![]() .
.

【题目】某市数学教研室对全市2018级15000名的高中生的学业水平考试的数学成绩进行调研,随机选取了200名高中生的学业水平考试的数学成绩作为样本进行分析,将结果列成频率分布表如下:
数学成绩 | 频数 | 频率 |
| 5 | 0.025 |
| 15 | 0.075 |
| 50 | 0.25 |
| 70 | 0.35 |
| 45 | 0.225 |
| 15 | 0.075 |
合计 | 200 | 1 |
根据学业水平考试的数学成绩将成绩分为“优秀”、“合格”、“不合格”三个等级,其中成绩大于或等于80分的为“优秀”,成绩小于60分的为“不合格”,其余的成绩为“合格”.
(1)根据频率分布表中的数据,估计全市学业水平考试的数学成绩的众数、中位数(精确到0.1);
(2)市数学教研员从样本中又随机选取了![]() 名高中生的学业水平考试的数学成绩,如果这
名高中生的学业水平考试的数学成绩,如果这![]() 的最小值;
的最小值;
(3)估计全市2018级高中生学业水平考试“不合格”的人数.