��Ŀ����
����Ŀ����ͼ![]() ��ijʮ��·�ڵĻ���������һ������뾶Ϊ
��ijʮ��·�ڵĻ���������һ������뾶Ϊ![]() ��Բ���λ��������ܰ����ߵ��ڲ����߹��ɱ߳�Ϊ
��Բ���λ��������ܰ����ߵ��ڲ����߹��ɱ߳�Ϊ![]() ��������.����Ҫ������Ա��ʹ�������ذ����ߵ��ڲ���в�������������
��������.����Ҫ������Ա��ʹ�������ذ����ߵ��ڲ���в�������������![]() ���ƶ��ٶ�Ϊ
���ƶ��ٶ�Ϊ![]() ������
������![]() ���ƶ��ٶ�Ϊ
���ƶ��ٶ�Ϊ![]() .������
.������![]() ������
������![]() �Ķ��ӹ��߱������赲���������
�Ķ��ӹ��߱������赲���������![]() ������
������![]() �ġ�ä������.
�ġ�ä������.



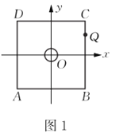
��1����ͼ![]() �������ߵ��ڲ����߹���������
�������ߵ��ڲ����߹���������![]() ������
������![]() �ڵ�
�ڵ�![]() ��������
��������![]() ��
��![]() �Ͼ����
�Ͼ����![]()
![]() �����������
�������ж�����![]() �Ƿ�������
�Ƿ�������![]() �ġ�ä�����У���˵�����ɣ�
�ġ�ä�����У���˵�����ɣ�
��2����ͼ![]() �������ߵ��ڲ����߹���������
�������ߵ��ڲ����߹���������![]() ������
������![]() �ӵ�
�ӵ�![]() �������
�������![]() �ƶ���ͬʱ����
�ƶ���ͬʱ����![]() �ӵ�
�ӵ�![]() �������
�������![]() �ƶ���������ƶ������У�����
�ƶ���������ƶ������У�����![]() ������
������![]() �ġ�ä�����е�ʱ��Ϊ���٣�
�ġ�ä�����е�ʱ��Ϊ���٣�
���𰸡���1���ǣ����ɼ���������2��![]() .
.
��������
��1������ƽ��ֱ������ϵ����õ�![]() ��
��![]() �����꣬�����ɵó�ֱ��
�����꣬�����ɵó�ֱ��![]() �ķ��̣����ԭ��
�ķ��̣����ԭ��![]() ��ֱ��
��ֱ��![]() �ľ��룬�ж�ֱ��
�ľ��룬�ж�ֱ��![]() �뻨������Բ��λ�ù�ϵ���ɴ˿ɵó����ۣ�
�뻨������Բ��λ�ù�ϵ���ɴ˿ɵó����ۣ�
��2������ƽ��ֱ������ϵ�����![]() ��
��![]() ��
��![]() ��
��![]() �����꣬��������
�����꣬��������![]() ������
������![]() �ġ�ä�����е�ʱ��Ϊ
�ġ�ä�����е�ʱ��Ϊ![]() ����
����![]() ��ʾ��
��ʾ��![]() ��
��![]() �����꣬�����ֱ��
�����꣬�����ֱ��![]() �ķ��̣�����Բ��
�ķ��̣�����Բ��![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() �ɵó�����
�ɵó�����![]() �IJ���ʽ�����
�IJ���ʽ�����![]() ��ȡֵ��Χ���ɴ˿ɵó����.
��ȡֵ��Χ���ɴ˿ɵó����.
��1��������ͼ![]() ��ʾ��ƽ��ֱ������ϵ����
��ʾ��ƽ��ֱ������ϵ����![]() ��
��![]() ������
������![]() ��
��
����ֱ��![]() �ķ�����
�ķ�����![]() ����
����![]() ��
��
��Բ��![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() ��
��
����Բ![]() ��ֱ��
��ֱ��![]() �ཻ��������
�ཻ��������![]() ������
������![]() �ġ�ä�����У�
�ġ�ä�����У�
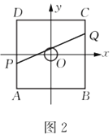
��2��������ͼ![]() ��ʾ��ƽ��ֱ������ϵ��
��ʾ��ƽ��ֱ������ϵ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
������֪��ʼʱ������![]() ������
������![]() �ġ�ä������.
�ġ�ä������.
��������![]() ������
������![]() �ġ�ä�����е�ʱ��Ϊ
�ġ�ä�����е�ʱ��Ϊ![]() ����
����![]() ��
��![]() ��
��
����ֱ��![]() ��б��
��� ��
��
��ֱ��![]() �ķ�����
�ķ�����![]() ����
����![]() ��
��
�Ӷ���![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ��� ��
��
������![]() �����
�����![]() �����ʱ��
�����ʱ��![]() ����
����![]() .
.
������![]() ������
������![]() �ġ�ä�����е�ʱ��Ϊ
�ġ�ä�����е�ʱ��Ϊ![]() .
.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�


