题目内容
如图，锐角三角形ABC内接于⊙O，∠ABC=60°，∠BAC=40°，作OE⊥AB交劣弧 |
| AB |
考点：圆內接多边形的性质与判定
专题：立体几何
分析：连接OC．由已知可得∠ACB=80°．利用垂径定理及其推论可得E为
的中点，
和
的度数．进而得到∠EOC的大小．利用等腰三角形即可得出∠OEC的大小．
|
| AB |
|
| BE |
|
| BC |
解答：
解：连接OC．如图所示，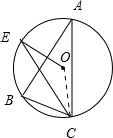
∵∠ABC=60°，∠BAC=40°，
∴∠ACB=80°．
∵OE⊥AB，
∴E为
的中点，
∴
和
的度数均为80°．
∴∠EOC=80°+80°=160°．
∴∠OEC=10°．
故答案为：10°
∵∠ABC=60°，∠BAC=40°，
∴∠ACB=80°．
∵OE⊥AB，
∴E为
|
| AB |
∴
|
| BE |
|
| BC |
∴∠EOC=80°+80°=160°．
∴∠OEC=10°．
故答案为：10°
点评：熟练掌握三角形的内角和定理、垂径定理及其推论、等腰三角形的性质是解题的关键．
练习册系列答案
相关题目
如图所示，在四面体A-BCD中，若截面PQMN是正方形，则在下列命题中错误的为（ ）
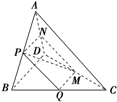
| A、AC⊥BD |
| B、AC∥截面PQMN |
| C、AC=BD |
| D、BD∥截面PQMN |
双曲线
-
=1上到定点（5，0）的距离是9的点的个数是（ ）
| x2 |
| 16 |
| y2 |
| 9 |
| A、0个 | B、2个 | C、3个 | D、4个． |
抛物线y=2x2的准线方程是（ ）
A、x=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
已知f（x+1）=3x+2，则f（x-1）=（ ）
| A、3x | B、3x-4 |
| C、3x-1 | D、3x+1 |