题目内容
将数列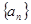 按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一
按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一
个数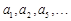 构成公差为
构成公差为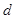 的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为
的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为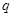 的等比数列.若
的等比数列.若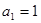 ,
,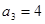 ,
,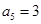 .
.
(1)求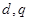 的值;
的值;
(2)求第 行各数的和
行各数的和 .
.
(1) ;(2)
;(2)
解析试题分析:(1)根据题意由等差数列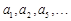 ,即
,即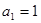 ,
,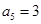 可求得等差数列的公差,从而根据等差数列求得
可求得等差数列的公差,从而根据等差数列求得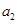 ,又由第二行起,每行各数按从左到右的顺序都构成公比为
,又由第二行起,每行各数按从左到右的顺序都构成公比为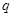 的等比数列,
的等比数列,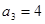 即可求得等比数列的公比.
即可求得等比数列的公比.
(2)根据等差数列求出每行的第一个数,又由题意可得每行的数列的个数为 ,公比
,公比 .所以由等比数列的前n项和的公式可求的结论.
.所以由等比数列的前n项和的公式可求的结论.
(1)依题意得 ,
, ,
,
所以 . 2分
. 2分
又 ,
, ,
,
所以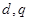 的值分别为
的值分别为 . 6分
. 6分
(2)记第 行第1个数为
行第1个数为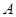 ,
,
由(1)可知: , 7分
, 7分
又根据此数表的排列规律可知:每行的总个数构成一个以1为首项,2为公差的等差数列,
所以第 行共有
行共有 个数, 9分
个数, 9分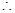 第
第 行各数为以
行各数为以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,
因此其总数的和 . 12分
. 12分
考点:1.等差数列的性质.2.等比数列的性质.3.分类递推的数学思想.

练习册系列答案
相关题目
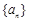 的公差
的公差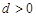 ,设
,设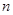 项和为
项和为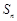 ,
,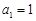 ,
,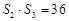
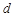 及
及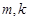 (
(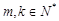 )的值,使得
)的值,使得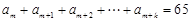 .
. 中,其前
中,其前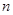 项和为
项和为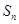 ,且
,且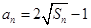 .
.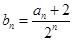 ,
,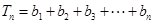 ,求证:
,求证: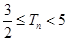 ;
;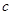 为实数,对任意满足成等差数列的三个不等正整数
为实数,对任意满足成等差数列的三个不等正整数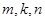 ,不等式
,不等式 都成立,求实数
都成立,求实数 的前n项和.
的前n项和.  , 且对所有正整数n, 有
, 且对所有正整数n, 有 . 判断
. 判断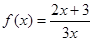 , 数列
, 数列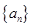 满足
满足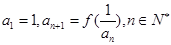 .
.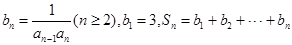 ,若
,若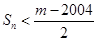 对一切
对一切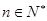 成立,求最小正整数m.
成立,求最小正整数m. 的前
的前 项和为
项和为 ,且
,且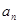 是
是 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前 ,证明:
,证明: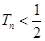 .
.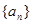 满足:
满足: 且
且
 .
.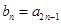 ,判断
,判断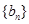 是否为等差数列,并求出
是否为等差数列,并求出 ;
;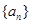 的前
的前 项的和为
项的和为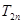 ,求
,求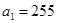 ,
,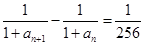
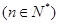 ,
,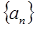 的通项公式
的通项公式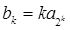 (
(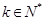 ),记数列
),记数列 的前k项和为
的前k项和为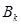 ,求
,求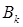 的最大值.
的最大值.