题目内容
数列 的前
的前 项和为
项和为 ,且
,且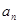 是
是 和
和 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: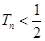 .
.
(1)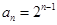 ,
,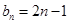 ;(2)证明见解析.
;(2)证明见解析.
解析试题分析:(1)由题中所给条件得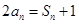 ,即
,即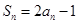 ,这是前
,这是前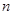 项和
项和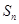 与项
与项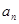 的关系,我们可以利用
的关系,我们可以利用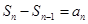 把此式转化为数列的项的递推式
把此式转化为数列的项的递推式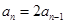 ,从而知数列
,从而知数列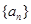 是等比数列,通项易得,这样等差数列的
是等比数列,通项易得,这样等差数列的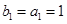 ,
,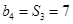 ,由基本量法可求得等差数列
,由基本量法可求得等差数列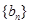 的通项公式;(2)数列
的通项公式;(2)数列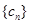 是由等差数列相邻两项相乘后取倒数所得,其前
是由等差数列相邻两项相乘后取倒数所得,其前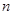 项和应该用裂项相消法求得,而当求得
项和应该用裂项相消法求得,而当求得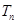 后,所要证的不等式就显而易见成立了.
后,所要证的不等式就显而易见成立了.
(1)∵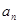 是
是 和
和 的等差中项,∴
的等差中项,∴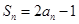
当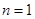 时,
时,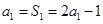 ,∴
,∴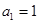
当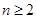 时,
时,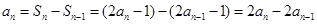 ,∴
,∴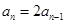 ,即
,即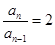
∴数列 是以
是以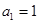 为首项,
为首项,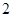 为公比的等比数列,∴
为公比的等比数列,∴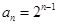 ,
,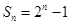
设 的公差为
的公差为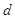 ,
,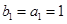 ,
,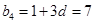 ,∴
,∴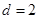 ∴
∴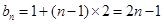 6分
6分
(2)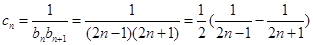
∴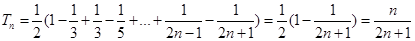
∵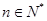 ,∴
,∴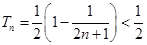 12分
12分
考点:(1)已知数列前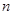 项和
项和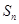 与项
与项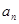 的关系,求通项公式,等差数列、等比数列通项公式;(2)裂项相消法求和与不等式。
的关系,求通项公式,等差数列、等比数列通项公式;(2)裂项相消法求和与不等式。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
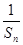 }的前n项和,问是否存在常数m,使Tn=m[
}的前n项和,问是否存在常数m,使Tn=m[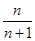 +
+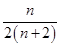 ],若存在,求m的值;若不存在,说明理由.
],若存在,求m的值;若不存在,说明理由. 中,
中, ,对于任意
,对于任意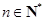 ,都有
,都有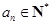 ,
,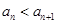 . 设
. 设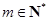 , 记使得
, 记使得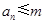 成立的
成立的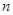 的最大值为
的最大值为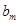 .
.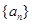 为1,3,5,7,
为1,3,5,7,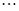 ,写出
,写出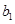 ,
,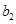 ,
,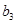 的值;
的值;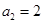 ,求
,求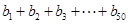 的值;
的值;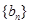 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列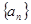 按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一
按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一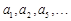 构成公差为
构成公差为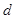 的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为
的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为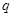 的等比数列.若
的等比数列.若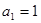 ,
,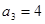 ,
,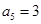 .
.
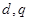 的值;
的值; 行各数的和
行各数的和 .
.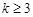 ,若项数为
,若项数为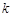 的数列
的数列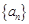 满足:对任意的
满足:对任意的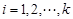 ,均有
,均有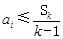 (其中
(其中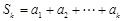 ),则称数列
),则称数列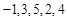 和
和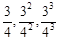 是否是“Γ数列”,并说明理由;
是否是“Γ数列”,并说明理由;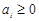 对
对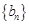 是公差为
是公差为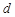 的无穷项等差数列,若对任意的正整数
的无穷项等差数列,若对任意的正整数 ,
,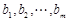
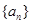 中,
中,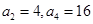 .
.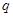 ;
;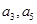 分别为等差数列
分别为等差数列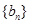 的第3项和第5项,求数列
的第3项和第5项,求数列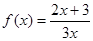 , 数列
, 数列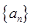 满足
满足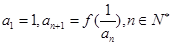 .
. ,若
,若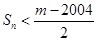 对一切
对一切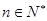 成立,求最小正整数m.
成立,求最小正整数m.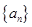 是各项为不同的正数的等差数列,
是各项为不同的正数的等差数列,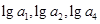 成等差数列,又
成等差数列,又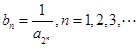 .
.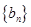 为等比数列;
为等比数列;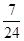 ,求数列
,求数列 为数列
为数列 的前
的前 项和,求
项和,求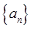 的前
的前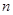 项和为
项和为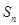 ,
,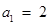 ,
,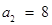 ,
, ,
,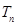 是数列
是数列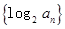 的前
的前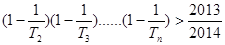 的最大正整数
的最大正整数