题目内容
已知等差数列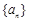 的公差
的公差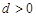 ,设
,设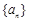 的前
的前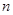 项和为
项和为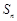 ,
,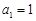 ,
,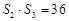
(1)求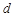 及
及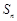 ;
;
(2)求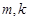 (
(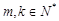 )的值,使得
)的值,使得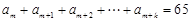 .
.
(1) ,
, (
( );(2)
);(2) ,
, .
.
解析试题分析:(1)根据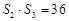 求出
求出 ,再由
,再由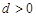 ,求出数列
,求出数列 的通项公式
的通项公式 ,用等差数列的求和公式求
,用等差数列的求和公式求 ;(2)由(1)的结论,把
;(2)由(1)的结论,把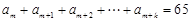 表示为
表示为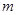 与
与 的等式,由条件
的等式,由条件
得出 ,解方程组求得结论.
,解方程组求得结论.
(1)由题意, ,
,
将 代入上式得
代入上式得 或
或 ,
,
因为 ,所以
,所以 ,从而
,从而 ,
, (
( ).
).
(2)由(1)知, ,
,
所以 ,
,
由 知,
知, ,
,
所以 ,所以
,所以 .
.
考点:数列的概念,通项公式,求和公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
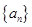 的首项
的首项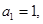 公差
公差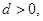 且
且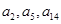 分别是等比数列
分别是等比数列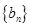 的
的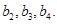
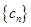 对任意正整数
对任意正整数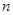 均有
均有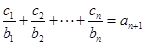 成立,求
成立,求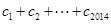 的值.
的值.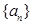 中,
中,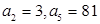 .
.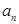 ;
;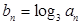 ,求数列
,求数列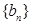 的前
的前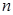 项和
项和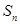 .
.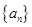 满足
满足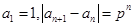 ,
,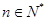 .
.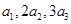 成等差数列,求
成等差数列,求 的值;
的值;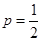 ,且
,且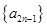 是递增数列,
是递增数列,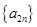 是递减数列,求数列
是递减数列,求数列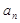 }的前
}的前 项和为
项和为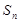 ,且满足
,且满足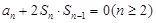 ,
,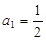 .
.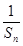 }是等差数列;
}是等差数列;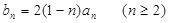 ,求证:
,求证: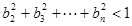 .
.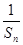 }的前n项和,问是否存在常数m,使Tn=m[
}的前n项和,问是否存在常数m,使Tn=m[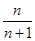 +
+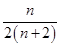 ],若存在,求m的值;若不存在,说明理由.
],若存在,求m的值;若不存在,说明理由. 中,
中,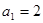 ,
,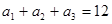 。
。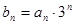 ,求数列
,求数列 的前
的前 项和
项和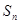
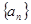 按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一
按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一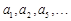 构成公差为
构成公差为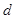 的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为
的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为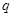 的等比数列.若
的等比数列.若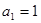 ,
,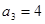 ,
,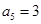 .
.
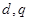 的值;
的值; 行各数的和
行各数的和 .
.