题目内容
在数列{an}中,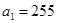 ,
,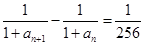
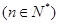 ,
,
(1)求数列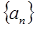 的通项公式
的通项公式
(2)设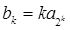 (
(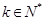 ),记数列
),记数列 的前k项和为
的前k项和为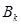 ,求
,求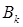 的最大值.
的最大值.
(1)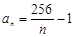 ;(2)466
;(2)466
解析试题分析:(1)由等差的定义可知数列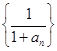 是以
是以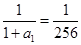 为首相,以
为首相,以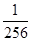 为公差的等差数列。用等差数列的通项公式可得的
为公差的等差数列。用等差数列的通项公式可得的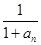 ,从而可得
,从而可得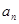 。(2)由(1)可知
。(2)由(1)可知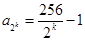 ,当
,当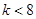 时
时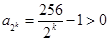 ,当
,当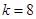 时
时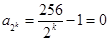 ,当
,当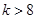 时
时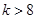 ,所以数列
,所以数列 的前7项或前8项和最大。因为
的前7项或前8项和最大。因为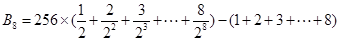 ,所以可用错位相减法求
,所以可用错位相减法求 ,再用等差前
,再用等差前 项和公式求
项和公式求 即可。
即可。
试题解析:(1)设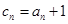 ,则数列
,则数列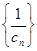 是一个等差数列,其首项为
是一个等差数列,其首项为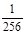 ,公差也是
,公差也是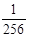 ,所以
,所以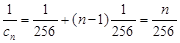 ,所以
,所以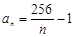 ,
,
(2)由(1)知当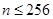 时,
时,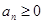 ,由
,由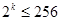 得
得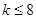 ,所以
,所以
数列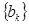 的前8项和
的前8项和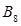 (或前7项和
(或前7项和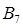 最大,因为
最大,因为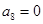 )最大,
)最大,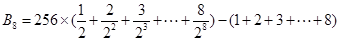 ,令
,令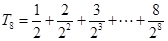 ,由错位相减法可求得
,由错位相减法可求得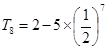 ,所以
,所以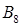 =
=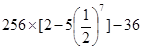 =466.即前7项或前8项和最大,其最大值为466.
=466.即前7项或前8项和最大,其最大值为466.
考点:1等差数列的定义及通项公式;2等差的前 项和公式;4错位相减法求数列的和。
项和公式;4错位相减法求数列的和。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
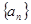 按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一
按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一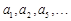 构成公差为
构成公差为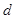 的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为
的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为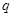 的等比数列.若
的等比数列.若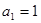 ,
,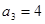 ,
,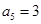 .
.
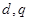 的值;
的值; 行各数的和
行各数的和 .
.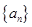 是各项为不同的正数的等差数列,
是各项为不同的正数的等差数列,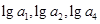 成等差数列,又
成等差数列,又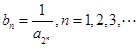 .
.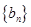 为等比数列;
为等比数列;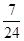 ,求数列
,求数列 为数列
为数列 的前
的前 项和,求
项和,求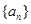 中,
中,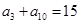 ,且
,且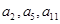 成等比数列.
成等比数列.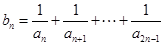 ,试比较
,试比较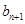 与
与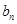 的大小,并说明理由.
的大小,并说明理由. 的前n项和为
的前n项和为 ,
,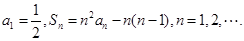
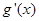 ;
;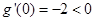 ,求证:
,求证: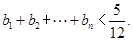
 }的首项为
}的首项为 a
a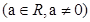 .设数列的前n项和为Sn,且对任意正整数n都有
.设数列的前n项和为Sn,且对任意正整数n都有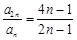 .
. 成等比数列?若存在,求出n和k的值;若不存在,请说明理由.
成等比数列?若存在,求出n和k的值;若不存在,请说明理由. 的前
的前 项和为
项和为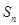 ,
,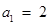 ,
,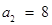 ,
, ,
,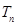 是数列
是数列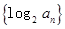 的前
的前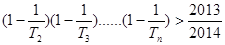 的最大正整数
的最大正整数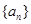 中,已知
中,已知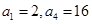 .
.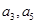 分别为等差数列
分别为等差数列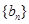 的第3项和第5项,试求数列
的第3项和第5项,试求数列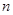 项和
项和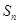 。
。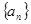
 中,其前
中,其前 项和为
项和为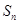 ,满足
,满足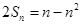 .
. (
(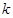 为正整数),求数列
为正整数),求数列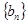 的前
的前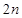 项和
项和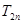 .
.